# 堆排序
🎢 了解堆排序 🔄
今天,我们将一探堆排序的奥秘,这个排序算法有点像给数据建个“乐园”,让我们看看它是如何运作的吧!
- 堆是一种特殊的树形数据结构,分为大根堆和小根堆。最大堆的每个节点都大于等于其子节点,而小根堆则相反。在堆排序中,我们通常使用大根堆。
# 算法流程
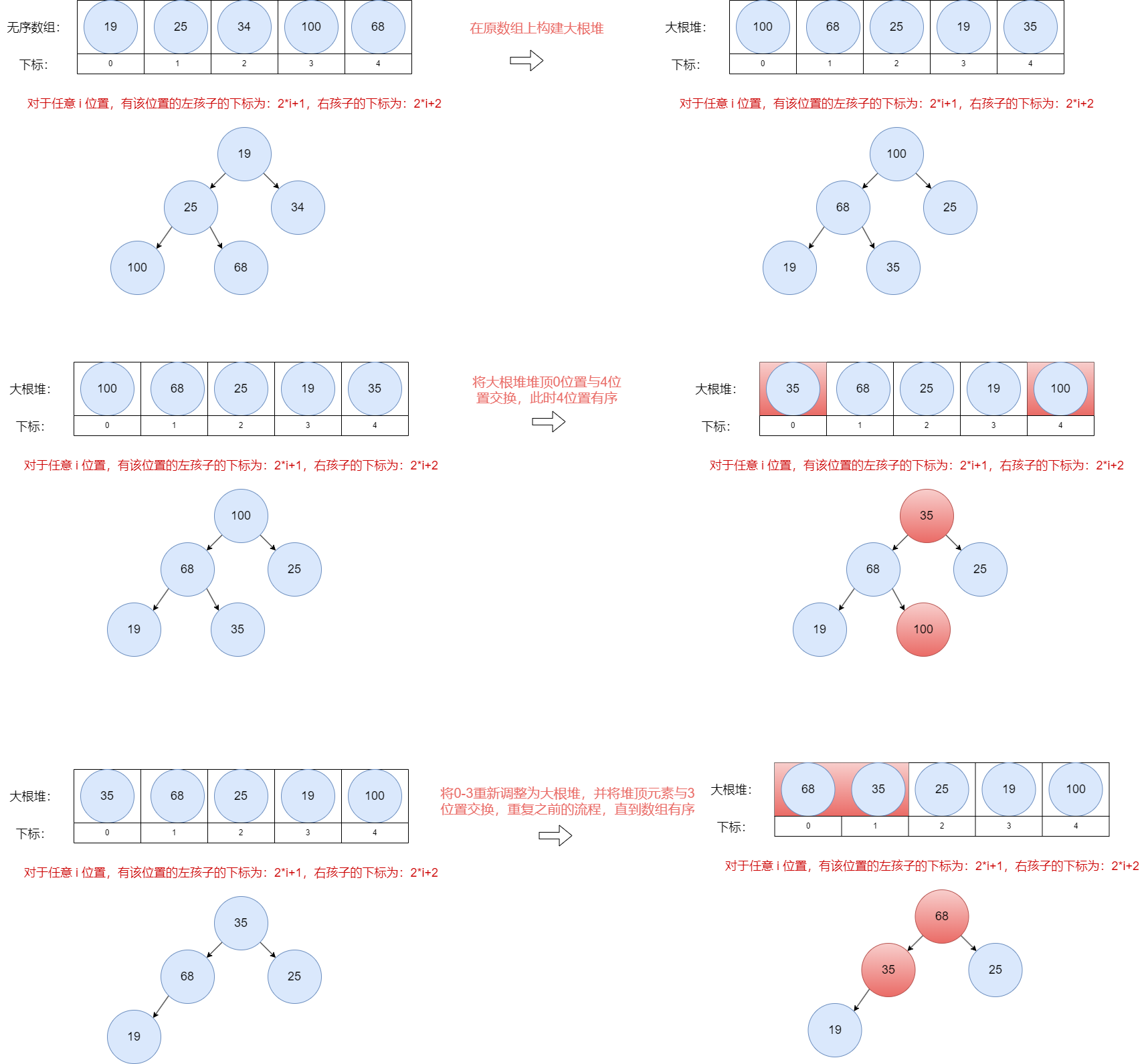
🔍 打磨排序的瑰宝:堆排序魔法步骤解析 ✨
🏰 打磨堆的宝藏
在这个排序魔法的第一步,我们要对原本无序的数组进行一次华丽的变身,把它调整成一个庞大的大根堆结构!这个大根堆就像是我们的宝藏府库,元素们在这里按照大小排列。
🌟 巅峰交换:堆顶元素独舞
接下来,让我们来一场巅峰交换!将大根堆的顶端,也就是最大的元素与数组最后的位置进行一场华丽的交换。这样一来,我们就在数组的最后铺下了一块有序的瑰宝之地。
🔄 魔法再现:堆的再次调整
不要急,魔法还没结束!我们要排除掉刚刚得到宝藏的最后一个位置,然后重新调整剩余的数据,让它们再次成为一个大根堆。这就像重新整理宝藏库,为下一轮瑰宝交换做好准备。
🔁 循环奏鸣:重复2-3的瑰宝之旅
然后,就是循环奏鸣的时候了!我们不停地重复步骤2-3,每一次都让最大的瑰宝跳到最后的位置。当我们的数组变得有序,整个排序的魔法就完成啦!
🚀 瑰宝集结,数组有序!
如此,经过一系列的华丽步骤,我们的无序数组就像是一座璀璨的城堡,每一步都是为了打磨出更加有序的瑰宝。
# 代码实现
package sort
import (
"traning/algorithm/utility"
)
func HeapSort(arr []int){
if arr == nil || len(arr) < 2 { return }
lenArr := len(arr)
// 从前往后在数组上insert建立大根堆,O(N*logN)
//for i:=0; i<len(arr); i++ {
// insert(arr, i)
//}
// 从后往前建立大根堆,O(N)
for i:=lenArr-1; i>=0 ; i-- {
heapify(arr, i, lenArr)
}
utility.Swap(arr, 0, lenArr-1)
lenArr--
for lenArr > 1 {
heapify(arr, 0, lenArr)
utility.Swap(arr, 0, lenArr-1)
lenArr--
}
}
func insert(arr []int, index int){
p := (index-1)/2
for arr[index] > arr[p] {
utility.Swap(arr, index, p)
index = p
p = (index-1)/2
}
}
// 拓展,原理参考二进制章节:
// p := (index-1) >> 1 可以这么写吗?
// -1: 1111111111111111111111111111111111111111111111111111111111111111
// 1: 0000000000000000000000000000000000000000000000000000000000000001
// >> 带符号右移,go中没有不带符号右移
func heapify(arr []int, index int, size int){
leftChild := (index<<1) | 1
bigger := leftChild
for leftChild < size {
bigger = leftChild
if leftChild+1 <size && arr[leftChild] < arr[leftChild+1] {
bigger = leftChild +1
}
if arr[index] > arr[bigger] {
break
}
utility.Swap(arr, index, bigger)
index = bigger
leftChild = (index<<1) | 1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
测试代码:
package sort
import (
"github.com/stretchr/testify/assert"
"sort"
"testing"
"traning/algorithm/utility"
)
func TestHeapSort(t *testing.T) {
a := assert.New(t)
testTime := 5000 // 测试次数
testArrMaxLen := 100 // 随机数组的最大长度[0, testArrMaxLen)
testArrMaxNum := 1000 // 随机数组中最大的数字[0, testArrMaxNum)
randomCreator := utility.GetRandomNumCreator() // 初始化随机数组生成器
for i:=0; i<testTime; i++ { // 开始测试,总共测试50万次
// 生成一个 长度为 [0, testArrMaxLen) 数字大小为 [0, testArrMaxNum) 的随机数组
ranArr := randomCreator.GetRandomArr(testArrMaxNum, testArrMaxLen)
// 拷贝数组用于进行校验
arr1 := utility.CopyArr(ranArr)
arr2 := utility.CopyArr(ranArr)
HeapSort(arr1) // 我们自己实现的选择排序,对arr1进行排序
sort.Ints(arr2) // 系统严格正确的排序方法,对arr2进行排序
a.True(utility.ArrEqual(arr1, arr2)) // 如果我们的排序的方式与严格正确的排序不一致,则我们的算法失败
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 复杂度分析
🚀 性能预测:预见未来的能力,通过对算法的时间和空间复杂度进行分析,我们能够更好地预测它在不同规模问题上的运行效率。
# 快排复杂度分析
insert建堆O(N*logN)或:
heapify建堆O(N)heapify调整堆O(N*logN)忽略常数项,整体时间复杂度O(N*logN)
insert 复杂度分析 -- 增大数据量分析法
数据量为N的时候,最差复杂度为:O(N*logN)
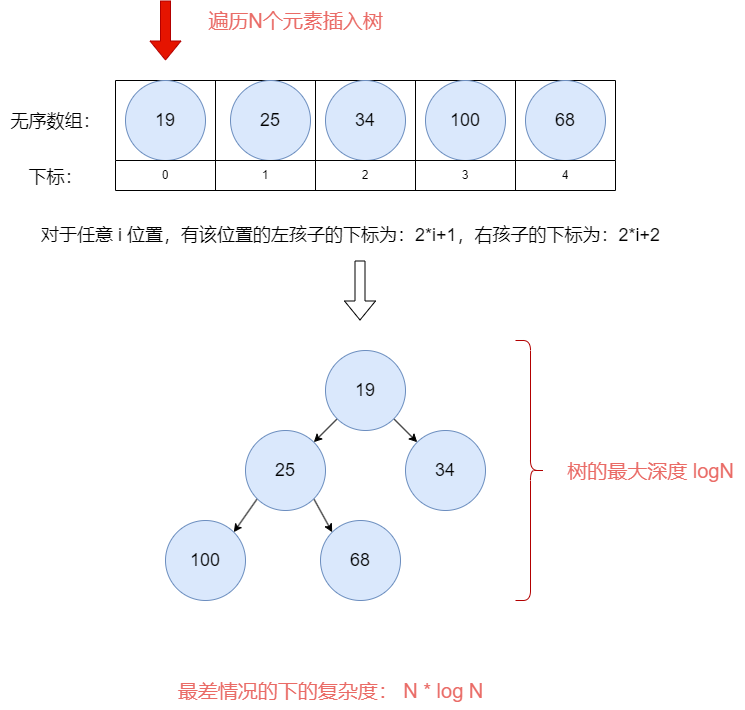
数据量为2N的时候,最差的复杂度为 O(N*logN):
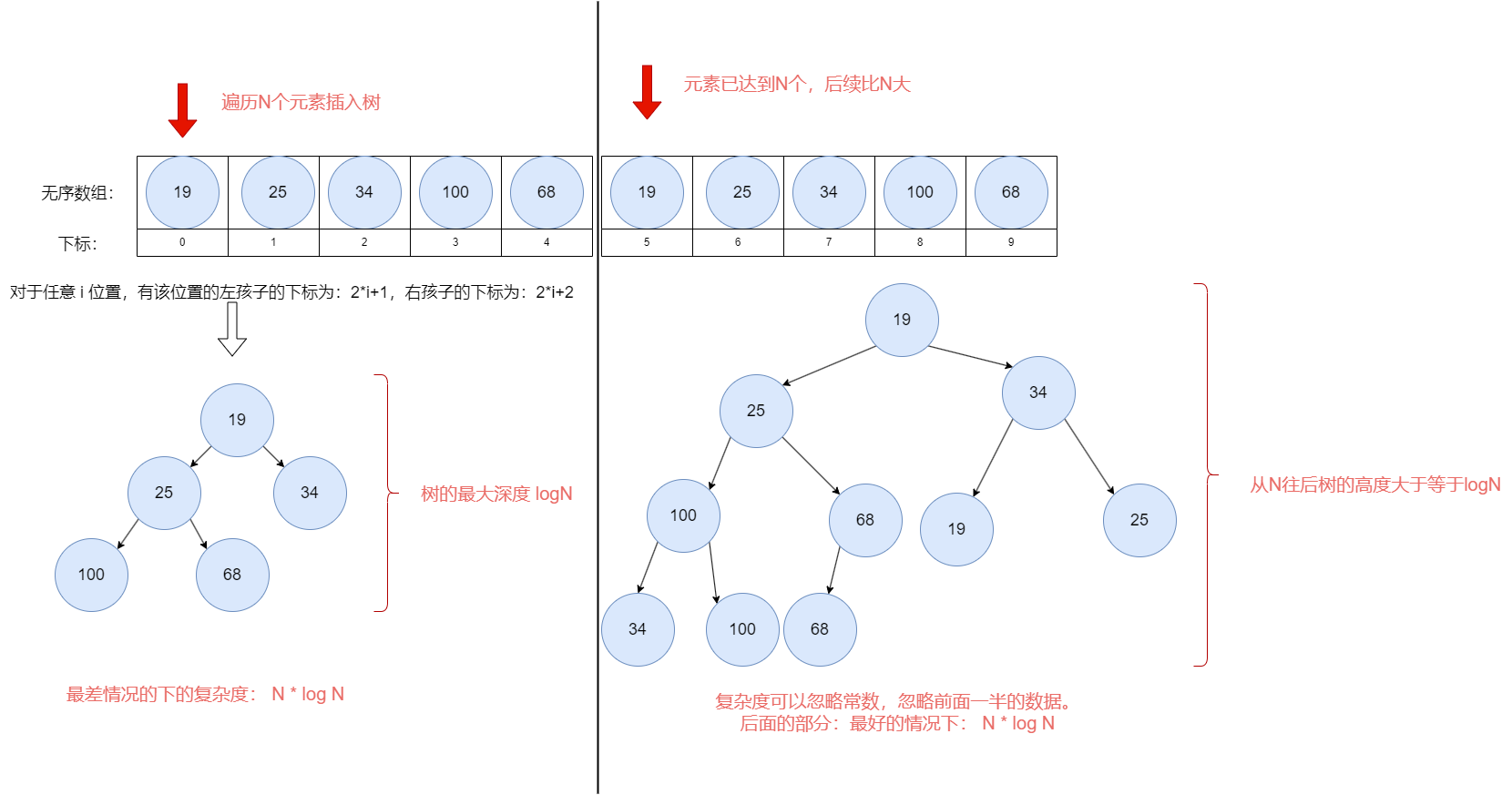
结论:N趋近无穷大的时候,整体的复杂度趋近于 O(N*logN)
# heapify建堆复杂度分析
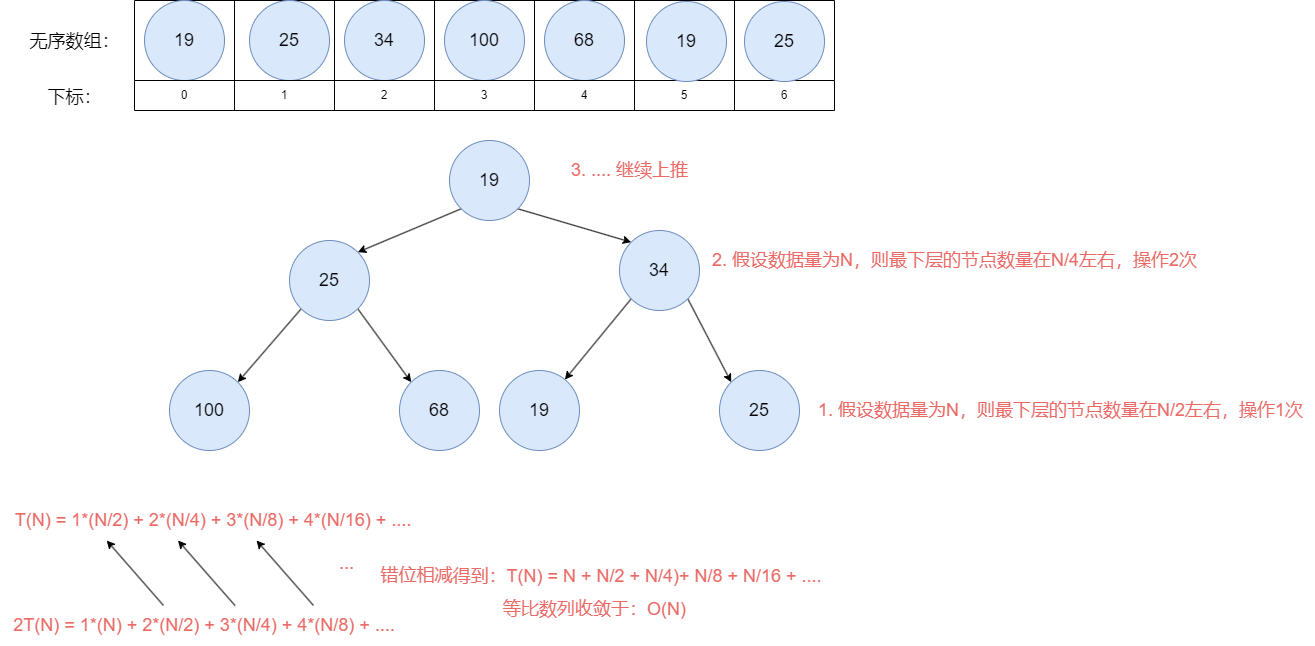
🏰倒序heapify的瑰宝🔄
heapify巧妙地选择了倒序建堆方式,其时间复杂度为:O(N)- 在这种策略下,从后往前的
heapify,仅需进行一次操作即可妙手回春大量的节点!🌟