图

概括

1. 由点的集合和边的集合构成

2. 虽然存在有向图和无向图的概念，但实际上都可以用有向图来表达

3. 边可能带有权值

难点

• 算法的步骤不难，难的地方在于数据结构比较复杂
• 相同的题目经常出现不同的数据结构来表达，所以一个算法可能不同题目有不同版本。

图示例

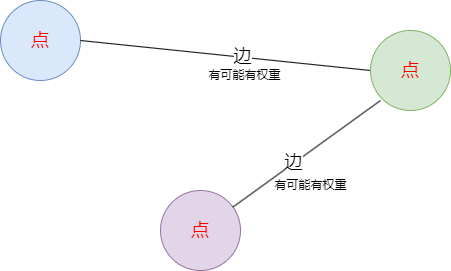
图-”森林“-示例

• ”森林“：存在多个图，多个图之间没有链接

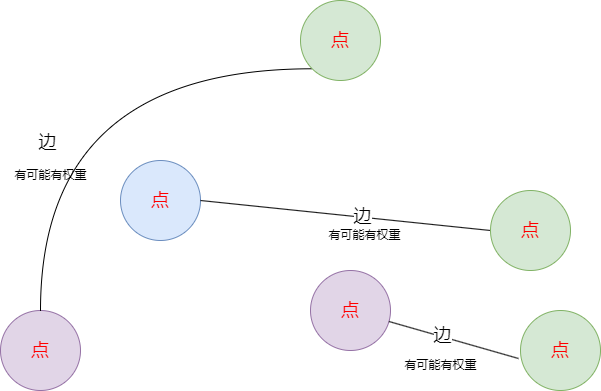
注意：图与二叉树的区别？

• 二叉树点之间的连接有严格的关系要求，如：子节点不可以从自身出发连接父节点
• 图的任意两个点之前都可以连接

无向图

以当前图为例子，任意连接的两点，从自身出发，都可以到连接的点，没有方向的要求，此时为无向图

有向图

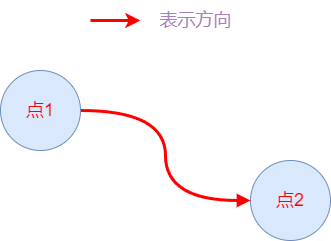
上图表示有向图，点1可以到达点2，但是点2不可以到达点1

统一表示

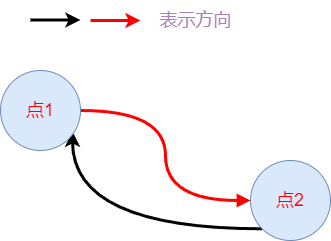
我们使用有向图的表达方式，在单向的表达上新增一个回去的方向，此时与无向图的本质一致。

图的常用表达方式

• 邻接表法
• 邻接矩阵法

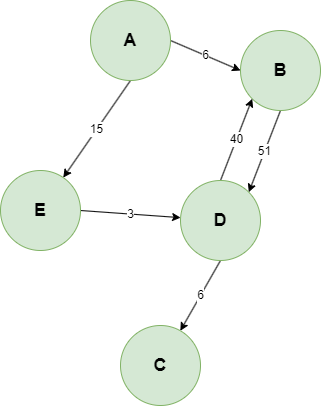
邻接表法

当前点	邻接点(点，权重)
A	(B，6) 、 (E，15)
B	(D, 51)
C	无
D	(C, 6)、(B, 40)
E	(D, 3)

邻接矩阵法

• 横纵都为点
• 表格内容为点到点的权重
• ∞ 无穷表示，两点之间不相邻

	A	B	C	D	E
A	0	6	∞	∞	15
B	∞	0	∞	51	∞
C	∞	∞	0	∞	∞
D	∞	40	6	0	∞
E	∞	∞	∞	3	0

推荐数据结构

点

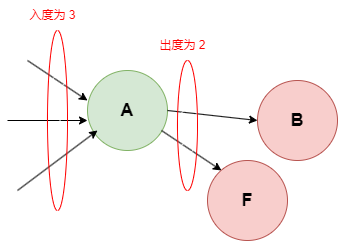
• 入度：可以到当前点的点数量
• 出度：当前点可以到的点的数量
• 直接相邻点：当前点可以到的点，在上图中则为 B、F
• 以当前点为出发点的线：在上图中为A到B、F的两条线

// 点的结构体
type Node struct {
	Val   int  // 点的序号，可以是数值，也可以是 A，根据具体情况定
	In    int  // 入度
	Out   int  // 出度
	Edges []*Edge // 以当前点为出发点的线
	Nexts []*Node // 直接相邻点
}

线

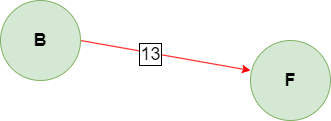
• 自身权重

• 出发点

• 目标点

// 边的结构体
type Edge struct {
	Weight  int    // 权重，如图则为 13
	From    *Node  // 出发点，如图则为 B
	To      *Node  // 目标点，如图则为 F
}

图

• 图由点和边构成
• 点使用唯一编号 映射
• 边采用集合的方式表示

// 图的结构体
type Graph struct {
	Nodes map[int]*Node       // 点集
	Edges map[*Edge]struct{}  // 边集
}

数据结构转换

目前有一张图，关系如下图所示：

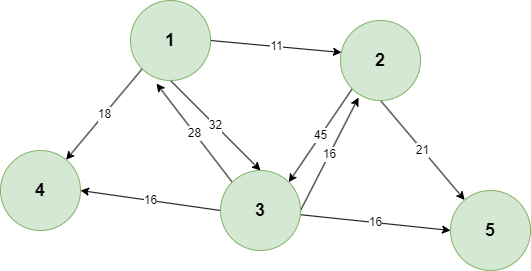
要求使用深度优先遍历与宽度优先遍历，来遍历这张图。

目前图的描述方式为一个二维数组，内容如下：

	chart := [][]int{
        // 第一个位置表示权重，
        // 第二个位置表示出发点的值
        // 第三个位置表示抵达点的值
		[]int{11, 1, 2},
		[]int{32, 1, 3}, 
		[]int{18, 1, 4}, 
		[]int{21, 2, 5},
		[]int{45, 2, 3},
		[]int{28, 3, 1},
		[]int{16, 3, 2},
		[]int{16, 3, 4},
		[]int{16, 3, 5},
	}

此时我们发现，我们之前说的数据结构体用不上了，那为什么要定好之前的数据结构呢？有什么好处呢？

答：好处在于，我们可以使用稳定的数据结构去学习图相关的算法，图相关的算法是不变的，但是图的表达形式千遍万化，我们不可能针对不同的数据结构都写一边算法。

那我们怎么使用之前的数据结构体呢？

答：我们只需要对不同的数据结构，写一个数据结构转换的函数即可，将不同的表达方式转换为我们熟悉的数据结构，并在我们熟悉的数据结构上实现算法。

以下针对本次例子的图，写一个数据结构体转换函数，内容如下：

func GenerateGraph(chart [][]int) Graph {
    // chart 图的二维数组，原始表达方式
    
    // 创建图，初始化图集，与边集
	graph := Graph{map[int]*Node{}, map[*Edge]struct{}{}}
    
    // 遍历原始数据，并进行数据转换
	for _, v := range chart {
        
        // 取出权重
		weight := v[0]
        
        // 拿到出发点
		from := v[1]
        
        // 拿到目的点
		to   := v[2]
        
        // 如果图中的节点不包含，出发节点，则创建节点，加入点集
		if !Contains(graph.Nodes, from) {
			graph.Nodes[from] = &Node{Val:from}
		}
        
        // 如果图中的节点不包含目标点，则创建节点，加入点集
		if !Contains(graph.Nodes, to) {
			graph.Nodes[to] = &Node{Val:to}
		}
        
        // 拿到出发点
		fromN := graph.Nodes[from]
        // 拿到目标点
		toN   := graph.Nodes[to]
        // 创建新的边
		NewEdge := &Edge{weight, fromN, toN}
        
        // 出发点的出度+1
		fromN.Out++
        // 出发点的直接邻点添加当前目标点
		fromN.Nexts = append(fromN.Nexts, toN)
        // 出发点的直接邻边添加当前边
		fromN.Edges = append(fromN.Edges, NewEdge)
        
        // 目标点的入度+1
		toN.In++
        
        // 图的边集加入当前边
		graph.Edges[NewEdge] = struct{}{}
	}
	return graph
}

func Contains(set map[int]*Node, node int)  (ok bool) {
	_, ok = set[node]
	return
}

宽度优先遍历

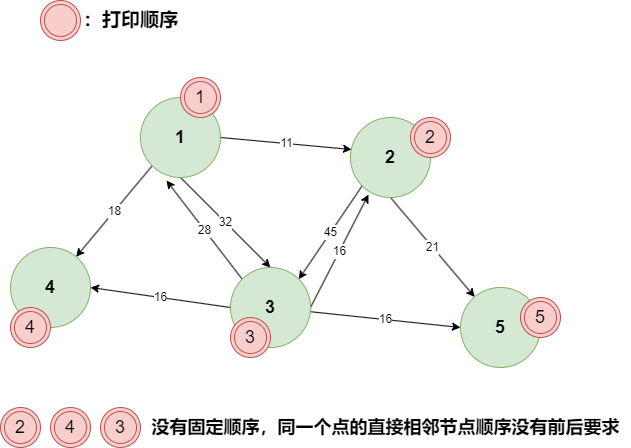
• 在图的宽度优先遍历中，同一个节点的直接相邻节点，之间的打印顺序，没有要求
• 在宽度优先遍历中，先打印当前节点，并将相邻节点加入队列中，从队列取出节点打印，然后继续将当前节点的相邻节点加入队列，一直循环知道队列为空
• 在图的数据结构中，两个点有可能互为直接相邻节点，所以需要预防死循环，需要加入set标记已经打印过的点

以下为宽度优先遍历的golang代码：

func GraphBFS(graph Graph){
    // graph 是我们经过转换的图
    
    // 创建队列
	queue := list.New()
    // 将1号节点放入队列中
	queue.PushBack(graph.Nodes[1])
    // 创建set标记加入过队列的节点
	nodeSet := map[*Node]struct{}{}
    // 标记1号已加入队列
	nodeSet[graph.Nodes[1]] = struct{}{}
	for queue.Len() > 0 {
        // 从队列取出节点
		node := queue.Remove(queue.Front()).(*Node)
        // 打印该节点
		fmt.Println(node.Val)
        // 遍历直接相邻节点
		for _, next := range node.Nexts {
            // 如果该节点没有进入过队列，则加入队列，并在set中标记该节点已进入队列
			if !Contains1(nodeSet, next) {
				queue.PushBack(next)
				nodeSet[next] = struct{}{}
			}
		}
	}
}

func Contains1(set map[*Node]struct{}, node *Node)  (ok bool) {
	_, ok = set[node]
	return
}

深度优先遍历

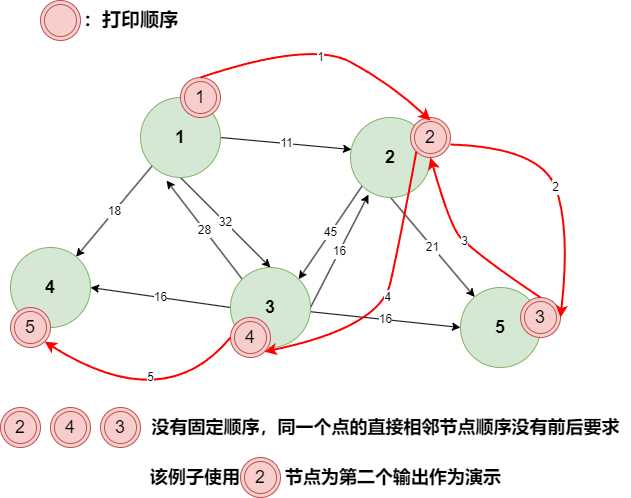
• 深度优先遍历，使用栈结构记录沿途的路径，对于遍历到的位置直接打印，打印后加入栈中，并标记。
• 循环从栈中取出节点，并遍历该节点的直接相邻节点，遍历过程中，如果遇到未进入过栈中的节点，则直接打印，并加入栈中，且跳出当前遍历
• 继续循环，以上步骤，知道栈为空，则遍历完毕

深度优先遍历的代码如下：

func GraphDFS(graph Graph) {
    
    // set 标记打印过的节点
	nodeSet := map[*Node]struct{}{}
    // 创建栈，记录深度遍历的路径
	stack := list.New()
    
    // 打印当前节点
	fmt.Println(graph.Nodes[1].Val)
    // 栈中加入1号节点
	stack.PushBack(graph.Nodes[1])
    // set 标记加入过栈的节点
	nodeSet[graph.Nodes[1]] = struct{}{}

	for stack.Len() > 0 { // 栈不为空代表没有遍历完
        
        // 取出栈顶节点
		node := stack.Remove(stack.Back()).(*Node)
        
        // 遍历栈顶节点，如果当前节点存在，则遍历直接相邻节点
		for _, next := range node.Nexts {
            // 如果直接相邻节点已经打印过了，则直接跳过
			if !Contains1(nodeSet, next) {
                // 没有打印过，则打印
                fmt.Println(next.Val)
                // 加入set标记已打印
                nodeSet[next] = struct{}{}
				// 遍历路径恢复，并退出
				stack.PushBack(node)
				stack.PushBack(next)
				break
			}
		}
	}
}