先序与后序遍历交集问题

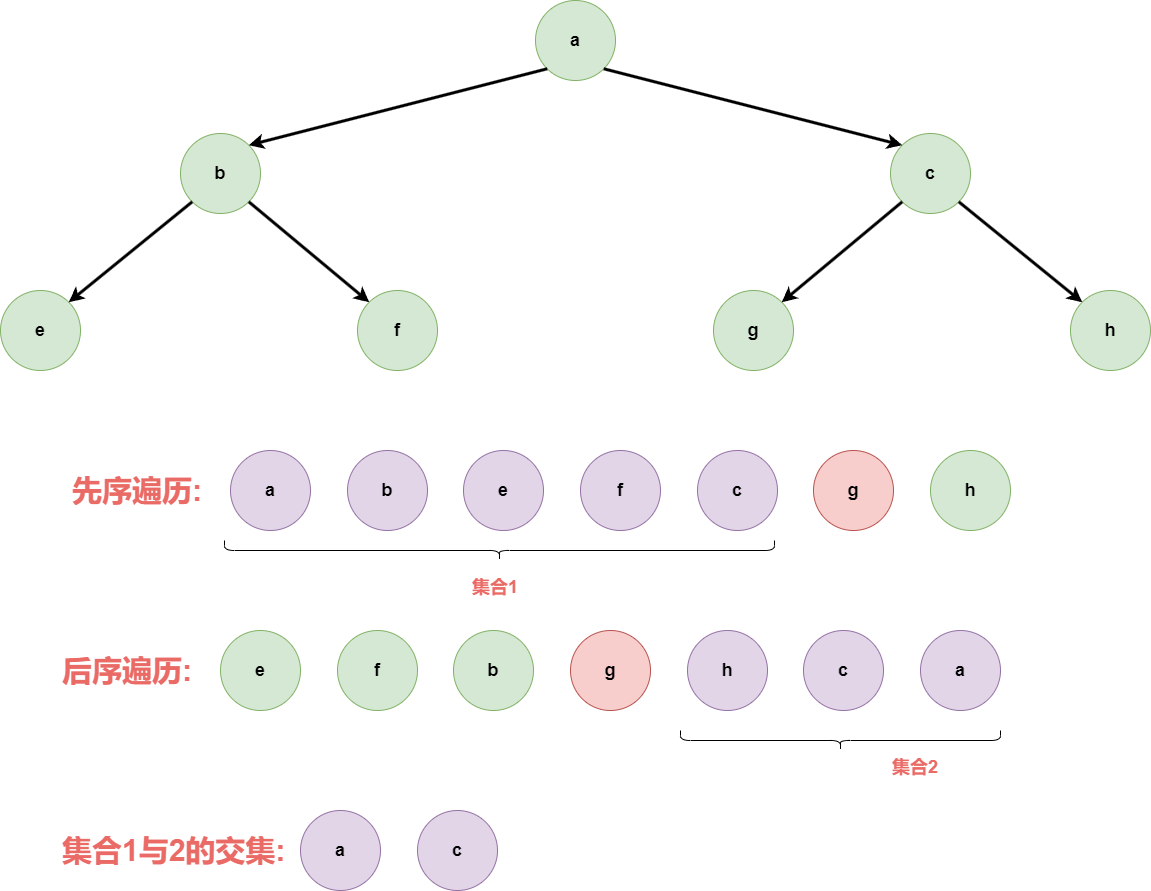
题目

对于上述的二叉树中节点g，先序遍历中g节点之前的集合为结合1，后序遍历中g节点之后的集合为集合2，两个结合的交集为节点a、c，这两个节点都为g节点的父节点，试证明对于任意的节点对应的集合交集都是该节点的父节点。

证明

证明该题目，只需要排除下面三种情况的节点即可

子节点

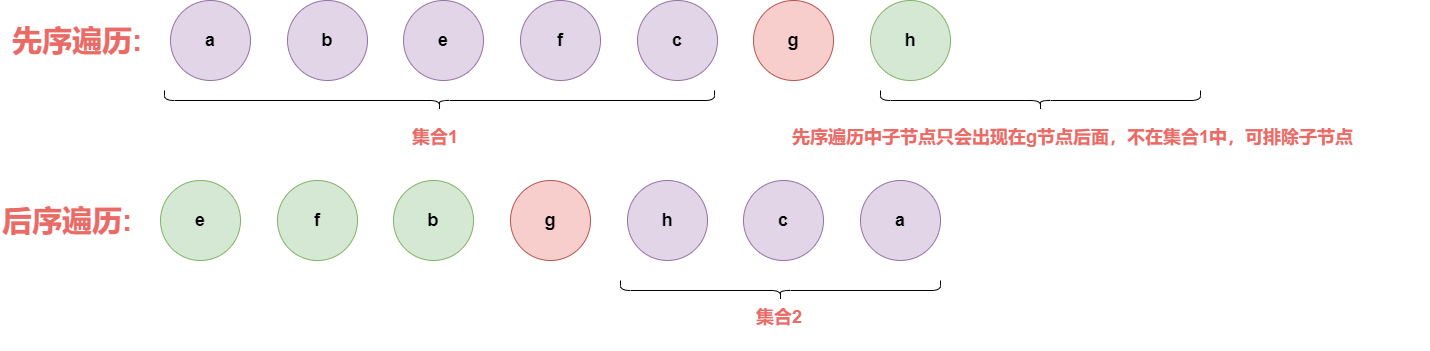
根据先序遍历的特性，先中左右，即任意节点的子节点只会出现在该节点后，即可排除交集中包含子节点

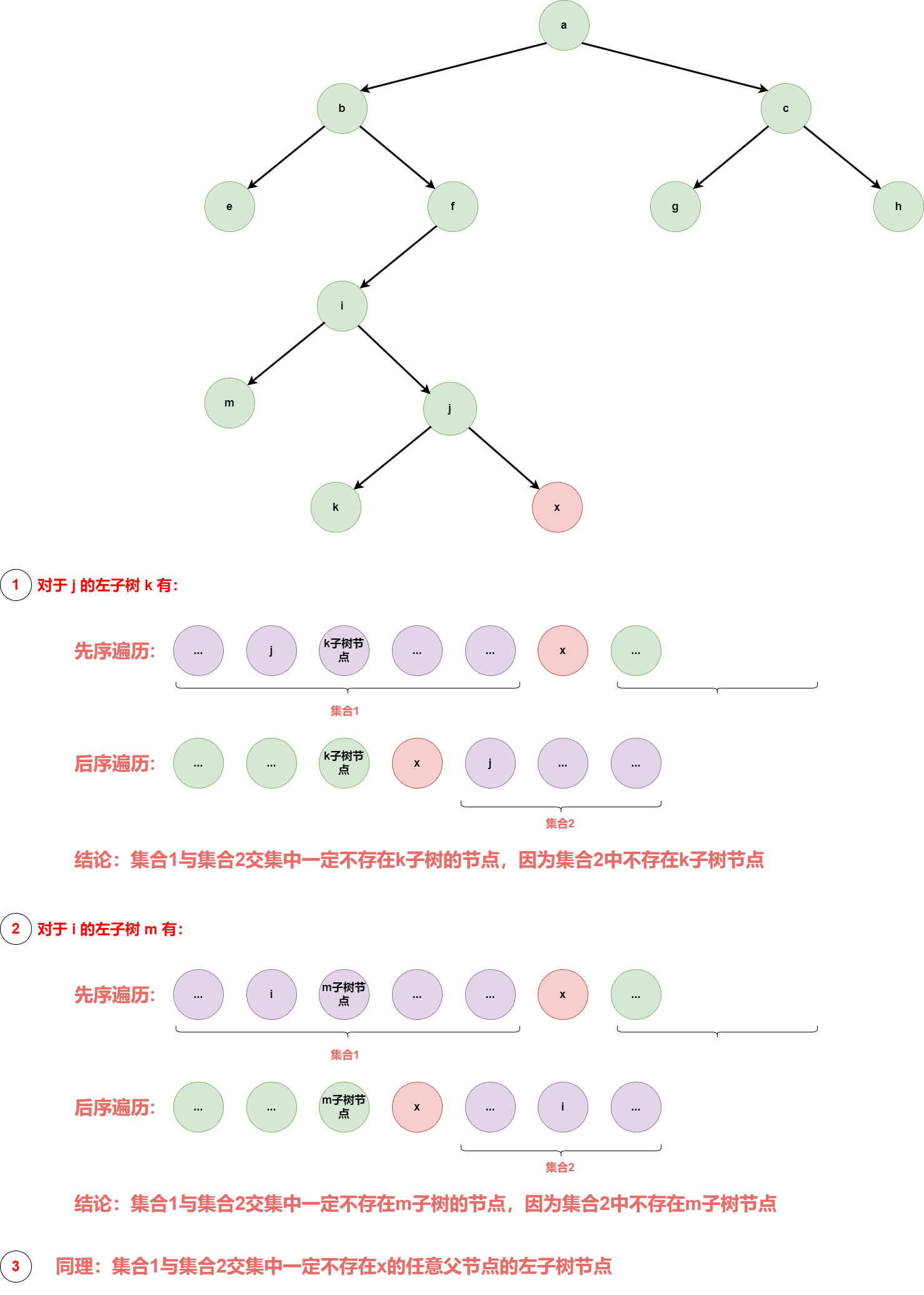
父节点的左子节点

下面证明x节点的先序与后序遍历前后的集合交集中一定不存在父节点的左子树：

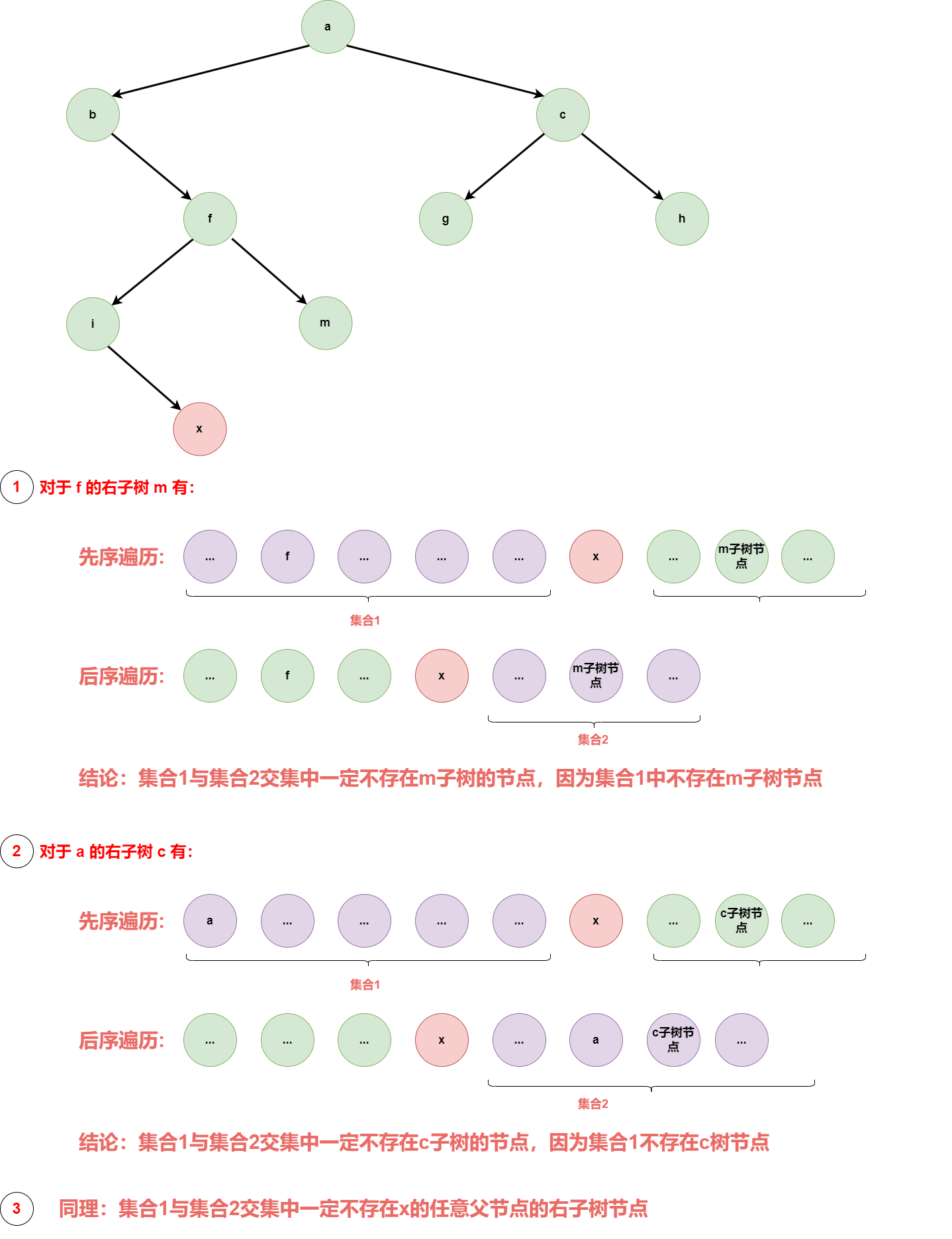
父节点的右子节点

下面证明x节点的先序与后序遍历前后的集合交集中一定不存在父节点的右子树：