# KMP
开始讲解KMP之前,我们先来看一个实际的题目:
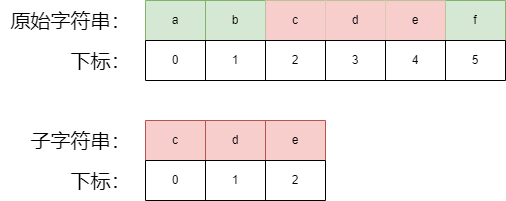
我们需要一个函数,该函数接收两个,参数,参数1 为原始字符串,参数2 为子字符串,该函数根据子字符串是否被原子字符串包含,若包含,则返回子字符串再原始字符串中开始的下标,如图上所示,该函数返回 2。
如果子字符串不在原始字符串中,则返回 -1
# 复杂度分析🤔
常规思路下,我们很容易想到,遍历每一个位置,然后开始与子字符串对比,如果成功匹配,则返回该位置的下标,如果遍历完,都没有匹配上子字符串,那么返回 -1
最差情况
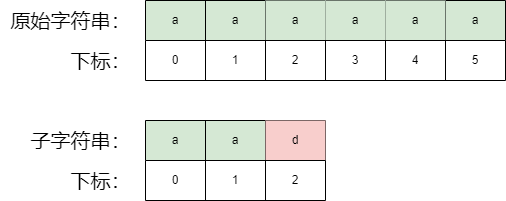
如果我们的数据状况,如上所示,原始字符串为 "aaaaaa" ,子字符串为 "aad",则我们使用常规思路去匹配子字符串,则在原始字符串中,我们每一个字符串的位置都将与子串进行匹配3次,而且最后一次为 "a" 匹配 "d",匹配失败。
这样的话,我们则总共匹配了 6 * 3 次,如果原始字符串为 N,子字符串长度为 M,则我们匹配了 N*M,所以算法复杂度为: O( N/*M)
# KMP 简介👇
kmp算法是由三位大牛Knuth、Morris和Pratt提出的(所以叫kmp),它的核心思想就是利用已经匹配过的字符信息来避免重复比较。👏
kmp算法是一种很厉害的字符串匹配算法,它可以帮助我们在一个长字符串中快速找到一个短字符串的位置。👍
# 为什么需要学习KMP🤔
学习了kmp算法,我们就可以用它来解决很多实际问题,比如字符串匹配、文本搜索、数据压缩等等。👏
比如说,我们可以利用kmp算法实现一个关键字搜索引擎,对于用户输入的查询关键字进行匹配,快速找到与之相关的内容。👍
这样就可以提高用户的搜索体验,让他们更容易找到自己想要的信息。👌
# 有什么收获🤩
- 👉更加熟练地处理字符串相关的问题
- 👉提高程序的效率
- 👉解决实际问题
# KMP的算法流程
我们以一个具体的例子体会,kmp算法的具体流程,我们需要用到下图的原始字符串,子字符串,next数组。
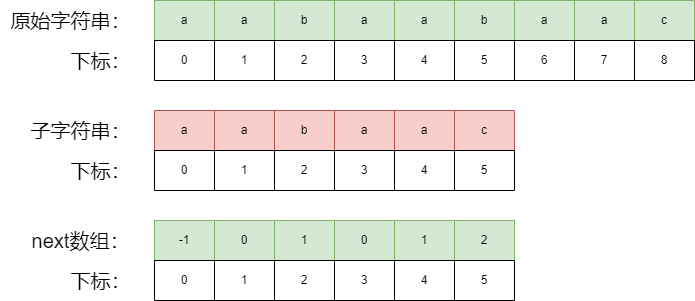
在开始之前,我们需要了解 最长相等的前后缀的概念,其实就是上图中的next数组
最长相等前后缀
对一个任意 i 位置的 字符,最长相等的前后缀是多少?
任意 i 位置的字符最长相等的前后缀的要求:
i 位置字符之前必须要有字符
最长相等前后缀要求不能是该字符串前面的所有字符串
前缀必须包含第一个字符
后缀必须包含最后一个字符
看以下具体的子字符对应的next数组的数据的由来:
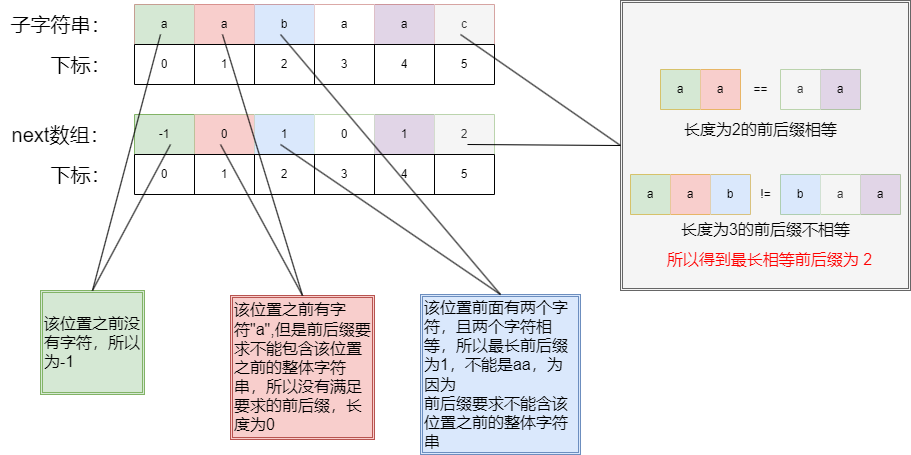
算法流程
第一步:与暴力匹配一样,我们选择原始字符串开始的位置,与子字符匹配,直到走到不匹配的位置。
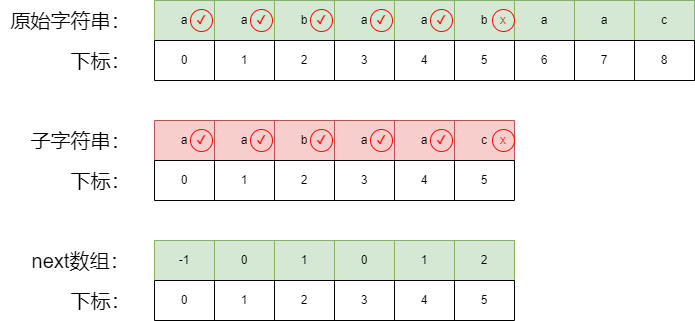
第二步:根据我们的next数组进行回退,从
b字符的位置开始匹配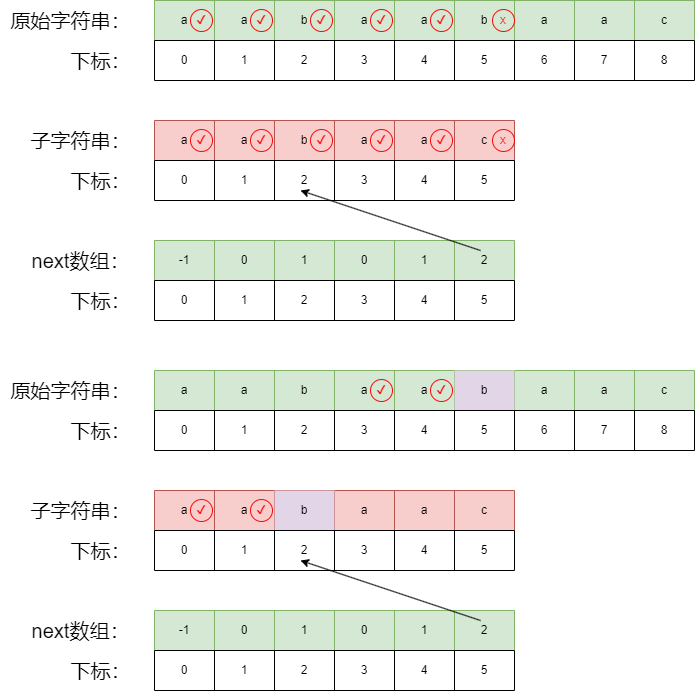
第三步:继续匹配,直到原始字符串越界或者子字符越界停止
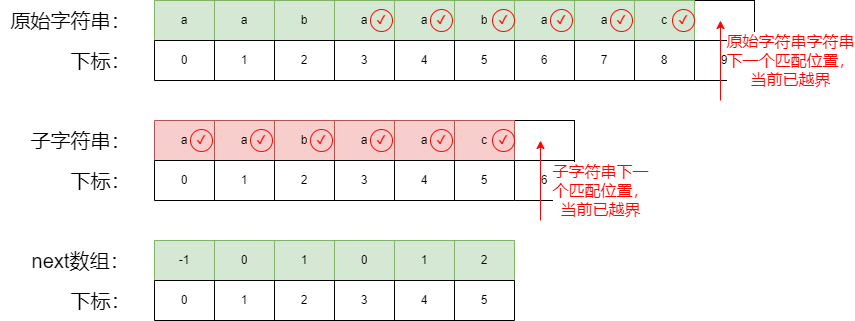
第四步:如何判断原始字符串与子字符串是否匹配,正确的匹配位置在哪里?上图可以知道:当原始字符串中,子字符串可以匹配上时,子字符串下一个可对比的位置一定是越界的,所以可以知道
- 当子字符串下一个位置已经越界时,直接返回原始字符串下一个对比位置(9)减去子字符下一个匹配的位置(6),得到3,满足我们的题目要求
- 当匹配流程走完,子字符串没有越界,但是原始字符串越界了,则表示没有匹配到子字符串,直接返回 -1
部分代码解读:
func FindIndex(originalString string, substring string) int {
if len(substring) > len(originalString) || substring == "" {
return -1
}
// 生成next数组,目前先不管,我们知道next数组的定义即可,后面会讲解next数组如何生成
next := GetNext(substring)
originalNextCompareIndex := 0 // 原始字符串下一个需要比较的位置,从0位置开始
substringNextCompareIndex := 0 // 子字符串下一个需要比较的位置,从0位置开始
// 只要两者的的对比位置,有一个越界了,则退出匹配
for originalNextCompareIndex < len(originalString) && substringNextCompareIndex < len(substring) {
if originalString[originalNextCompareIndex] == substring[substringNextCompareIndex] {
// 如果对比的位置,字符串相等,则两者的比较位置都加1
originalNextCompareIndex++
substringNextCompareIndex++
} else if next[substringNextCompareIndex] != -1 {
// 如果不相等,且子字符串的next数组中的下标可回退,则将子字符串的对比位置回退至 next 数组指向的下标
substringNextCompareIndex = next[substringNextCompareIndex]
} else {
// next 数组不能回退,则代表第一个字符串与原始字符串的当前位置都不相等
// 所以原始字符串的 index + 1,继续下一次匹配
originalNextCompareIndex++
}
}
// 如果子字符串的匹配位置越界了,则返回 原始字符串的下一个匹配位置减去子字符串的下一个匹配位置
if substringNextCompareIndex == len(substring) {
return originalNextCompareIndex - substringNextCompareIndex
}
// 如果子字符串没有越界,证明原始字符串中不包含子字符串,则直接返回 -1
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 加速的本质
子字符串下一次对比位置回退
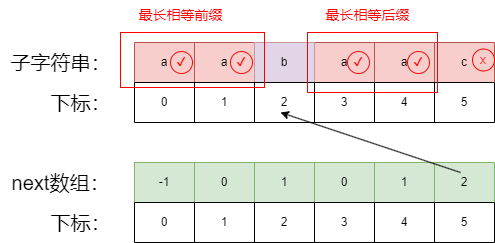
在暴力匹配过程中,当我们匹配不上时,我们直接回退对比位置到下标 0,但是在kmp中,我们借助 next 数组,我们可以知道,当5位置的c不匹配时,我们可以将下一个匹配位置直接回退到 2 而不是 0,因为 3,4 位置的 aa 已经通过匹配了,此时 0,1 位置与 3,4位置相等,所以0,1位置我们不用匹配,这个过程可以跳过,直接从2位置开始继续与原始字符串匹配。
回退时原始串的实际匹配的起始位置
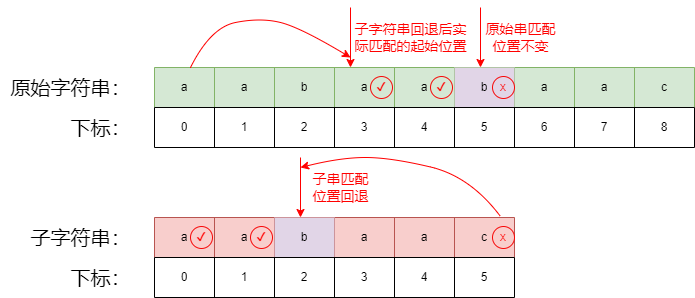
当子字符串回退到 2 开始匹配,但是原始字符串匹配位置不变时,相当于原始字符串匹配的开头位置来到3位置,直接跳过了 1, 2 的位置,相比暴力匹配会更快。
但是为什么 1,2 位置开头不可能匹配出子字符串呢?
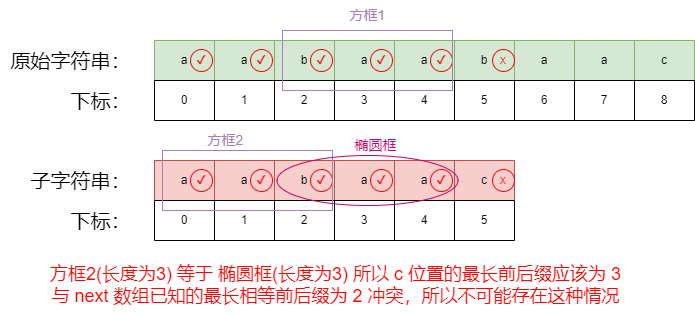
上图假设 原始字符串中存在 2 位置开头的字符串与 子字符串完全匹配,则方框1中的3个字符,与方框2中的3个字符一定相等,因为假设2位置开头存在与子字符串相匹配的字符。
由于之前我们已经匹配过原始字符串中 2-4 的字符,与 子字符串中 2-4 的字符,该位置3个字符相等。
所以,我们通过假设可以知道子字符串中 0-2 位置的字符,与2-4的字符相等,此时满足前后缀字符串的定义,可以知道 5 位置的最长相等前后缀为 3。
由于我们5位置已知的最长前后缀为2, 与我们的通过假设得出的 3 相矛盾,所以假设不成立。
通过上述假设,我们可以得出 2 位置开头不可能可以匹配出子字符串,1位置同理。
# Next数组的生成
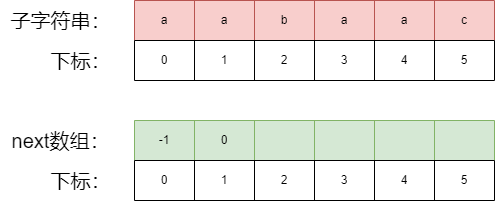
**第一步初始化next数组:**上图next数组中,前两个位置是固定的,0位置之前没有字符串,不存在最长相等前后缀的概念,填充 -1。1位置前只有一个字符串,但是最长相等前后缀要求最长前后缀不能等于字符之前所有的字符串,所以该位置填充 0。
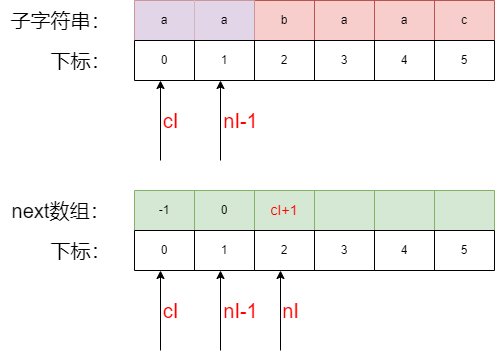
第二步填充next数组2位置:
nI 的含义:next数组当前需要填充的位置
cI有两个含义:
- 指向 与
nI-1尝试匹配的字符串 - 匹配失败后,指向next数组中可跳转的位置
步骤:
- 比较子字符串中
cI与nI -1的字符,a 等于 a,next 字符串的nI位置即等于cI+1,所以2位置填cI+1=1 cI++且nI ++
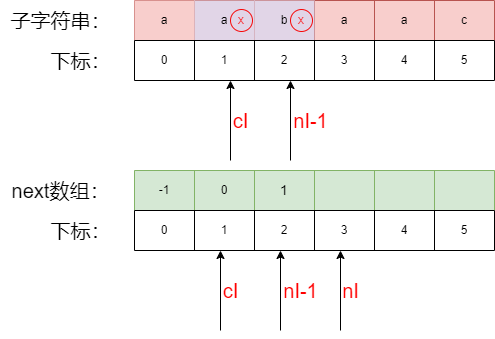
第三步填充next数组 3 位置:
步骤:
cI指向的a不等于nI -1指向的b,此时cI需要回退cI根据next数组回退cI=next[cI],所以cI回退为0
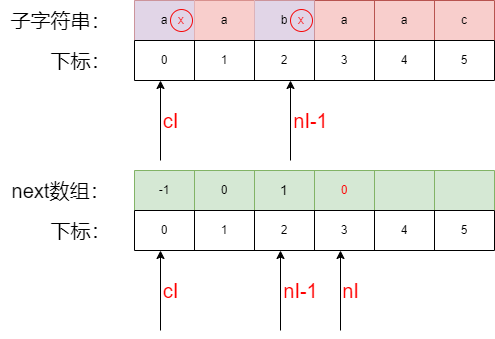
- 回退后,继续对比子字符中的
cI与nI -1的字符,此时还是不相等 - 此时
cI为0在 next 中的0位置指向-1已经无法回退 - 不存在与
nI-1匹配的字符,所以,next中nI的位置填写0 - 填写完当前的
nI后执行nI++,进行下一次计算
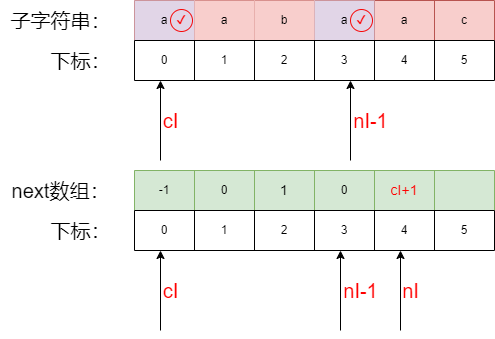
第三步填充next数组 4 位置:
步骤:
- 比较子字符串中
cI与nI -1的字符,a 等于 a,next 字符串的nI位置即等于cI+1,所以2位置填cI+1=1 cI++且nI ++
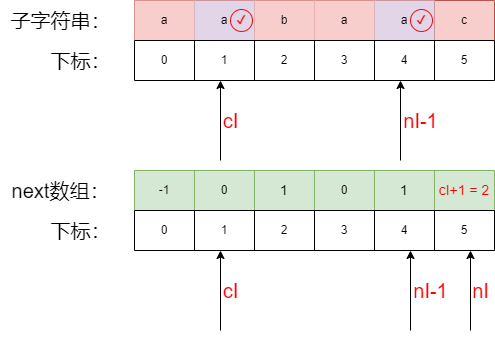
第四步填充next数组 5 位置:
步骤:
- 比较子字符串中
cI与nI-1的字符,a 等于 a,next 字符串的nI位置即等于cI+1,所以2位置填cI+1=2 cI++且nI ++
代码解析
func GetNext(match string) []int {
if len(match) == 1 {
return []int{-1}
}
// 初始化 0,1 位置
next := make([]int, len(match))
next[0] = -1
next[1] = 0
nI := 2 // next数组下一个生成的位置的下标
cI := 0 // 1. 与 nI-1 对比的位置下标 2. next回退的下标
for nI < len(match) {
if match[nI-1] == match[cI] { // 字符相等直接填写
next[nI] = cI +1
nI++
cI++
} else if next[cI] != -1 { // 字符不相等时回退
cI = next[cI]
} else { // 无法回退时,直接赋0,且到下一个位置
next[nI] = 0
nI++
}
}
return next
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 复杂度证明
算法流程中的for循环复杂度分析
func FindIndex(originalString string, substring string) int {
// O(1)
if len(substring) > len(originalString) || substring == "" {
return -1
}
// ? 先不管
next := GetNext(substring)
// O(1)
originalNextCompareIndex := 0
substringNextCompareIndex := 0
// O(N)
for originalNextCompareIndex < len(originalString) && substringNextCompareIndex < len(substring) {
if originalString[originalNextCompareIndex] == substring[substringNextCompareIndex] {
originalNextCompareIndex++
substringNextCompareIndex++
} else if next[substringNextCompareIndex] != -1 {
substringNextCompareIndex = next[substringNextCompareIndex]
} else {
originalNextCompareIndex++
}
}
// O(1)
if substringNextCompareIndex == len(substring) {
return originalNextCompareIndex - substringNextCompareIndex
}
return -1
}
/*
for 循环进入了多少次呢?
originalNextCompareIndex 上限是 N
originalNextCompareIndex - substringNextCompareIndex 上限是 N
for 循环中有三个分支,每次循环走其中一个分支
originalNextCompareIndex (originalNextCompareIndex - substringNextCompareIndex)
分支一 上升 不变
分支二 不变 上升
分支三 上升 上升
每次进入循环必定进入其中一个分支,最差情况 会计算 2N 次,进入分支一N次,进入分支二N次,所以该部分的算法复杂度为O(N)
*/
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
next数组for循环的复杂度分析
func GetNext(match string) []int {
...O(1)
nI := 2
cI := 0
O(n?)
for nI < len(match) {
if match[nI-1] == match[cI] {
next[nI] = cI +1
nI++
cI++
} else if next[cI] != -1 {
cI = next[cI]
} else {
next[nI] = 0
nI++
}
}
...O(1)
}
/*
for 循环进入了多少次呢?
nI 上限是 M
nI - cI 上限是 M
for 循环中有三个分支,每次循环走其中一个分支
nI (nI-cI)
分支一 上升 不变
分支二 不变 上升
分支三 上升 上升
每次进入循环必定进入其中一个分支,最差情况 会计算 2M 次,进入分支一N次,进入分支二N次,所以该部分的算法复杂度为O(M)
*/
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
算法整体复杂度
求next数组,O(M)
匹配过程,O(N)
其余过程 O(1)
总复杂度 = O(M) + O(N) + O(1) = O(N)
2
3
4
# KMP完整代码
func FindIndex(originalString string, substring string) int {
if len(substring) > len(originalString) || substring == "" {
return -1
}
next := GetNext(substring)
originalNextCompareIndex := 0
substringNextCompareIndex := 0
for originalNextCompareIndex < len(originalString) && substringNextCompareIndex < len(substring) {
if originalString[originalNextCompareIndex] == substring[substringNextCompareIndex] {
originalNextCompareIndex++
substringNextCompareIndex++
} else if next[substringNextCompareIndex] != -1 {
substringNextCompareIndex = next[substringNextCompareIndex]
} else {
originalNextCompareIndex++
}
}
if substringNextCompareIndex == len(substring) {
return originalNextCompareIndex - substringNextCompareIndex
}
return -1
}
func GetNext(match string) []int {
if len(match) == 1 {
return []int{-1}
}
next := make([]int, len(match))
next[0] = -1
next[1] = 0
nI := 2
cI := 0
for nI < len(match) {
if match[nI-1] == match[cI] {
next[nI] = cI +1
nI++
cI++
} else if next[cI] != -1 {
cI = next[cI]
} else {
next[nI] = 0
nI++
}
}
return next
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49