堆

为了更方便我们理解堆的作用，我们假设有下面一个场景。我们现在有五个人，每个人的重量都不一样，我们还有一个屋子，屋子可以装下所有人，但是只能一个一个的进入屋子，并且出来时也只能一个一个出来。

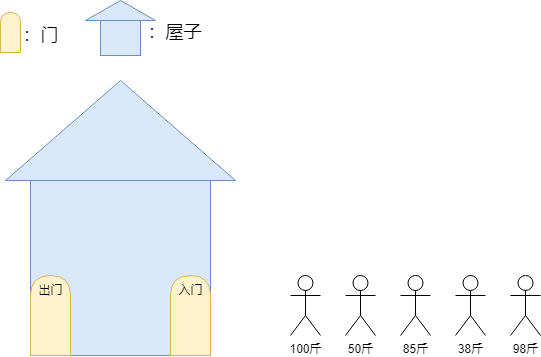
我们的屋子在有人进入的时候需要组织这些人在屋子内部排队，屋子还有一个功能就是，可以要求当前屋子内是最重的人先出，还是最轻的人先出来。但是屋子一旦建好，只能拥有其中一个功能，要不就是重的人先出来，要不就是轻的人先出来。

假设现在屋子出来的规则是，屋子内最轻的先出来，此时屋子已经进了三个人：

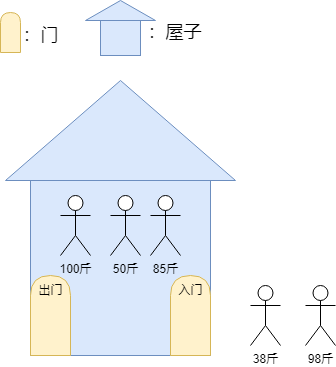
现在要求屋子出来人，则此时最轻的是50斤的人，先出来：

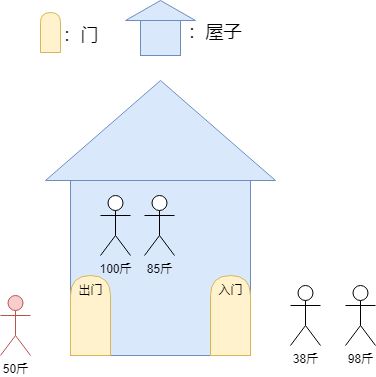
若此时38斤的人进入屋子，则此时如下图所示：

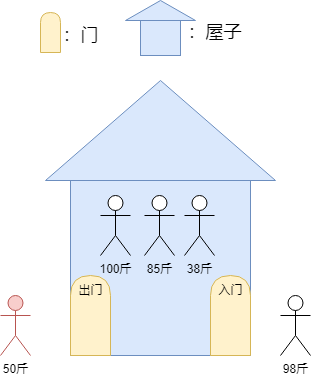
此时要求屋子出来人，则 38斤的人是屋子里最请的人，则38斤的人需要出来，如下：

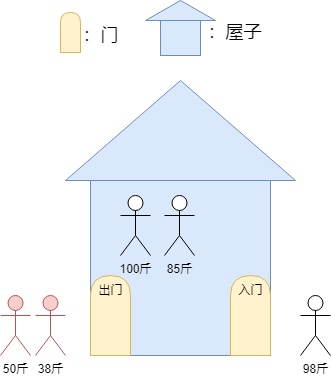
理解到这里，其实我们说的堆的功能就和上面的屋子的功能一样，需要在内部保证数据的顺序，也根据是最大的先出，还是最小的先出来分为大根堆和小根堆

根据出门和入门我门知道，堆还应该有两个方法，一个是进堆和一个是出堆。

在建堆的时候，还需要规定，出堆的规则，并且规定堆的大小，保证堆可以装下所有的人。

算法步骤

堆内部具体的排序原理，我们以下面五个元素，依次进入小根堆后，再依次出小根堆为例子，看看堆内部是如何进行排序及调整的，我们当前有五个元素，小根堆为黄色区域，目前元素并未进入小根堆，小根堆为空。

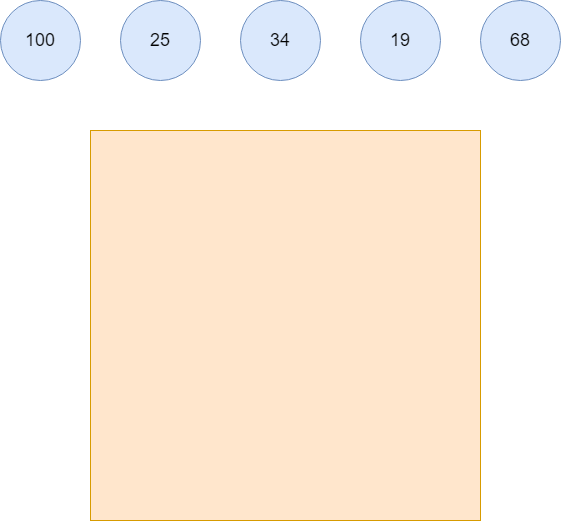
1. 元素100进入小根堆，作为堆顶元素。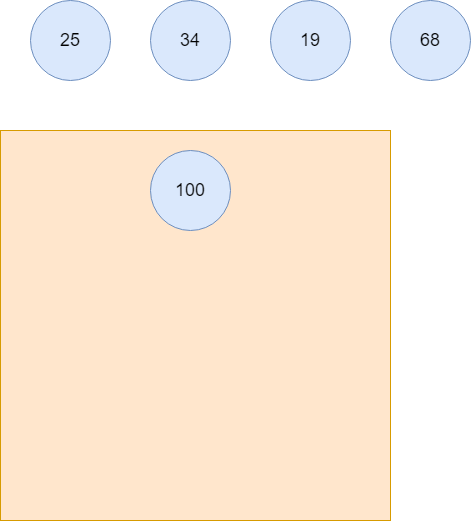

   

2. 元素25插入堆中，作为元素100的左孩子，以二叉树的形式呈现。插入后，需要判断其与父亲节点的关系，如果比父亲节点小则与父亲节点交换位置。（这是小根堆的规则，如果是大根堆，则是如果比父亲节点大，才与父亲节点交换位置）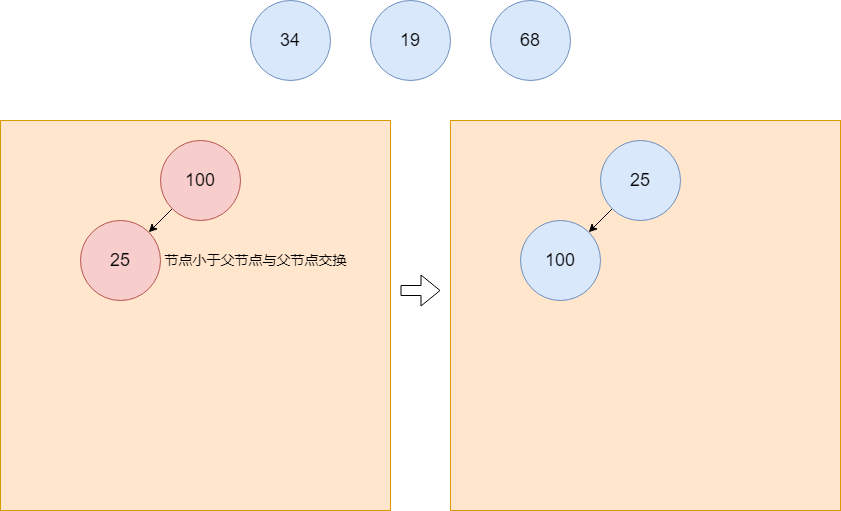

   

3. 元素34插入堆中，作为元素100的右孩子，以二叉树的形式呈现。插入后大于父节点的值，无需变更位置。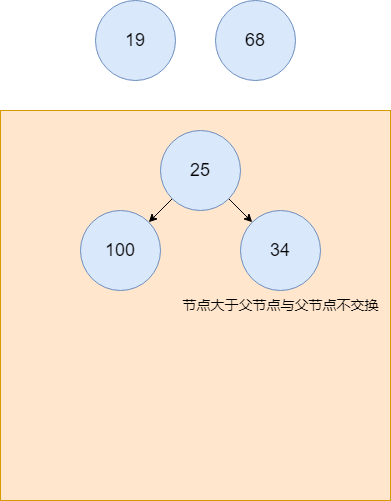

   

4. 元素19插入堆中，作为元素25的左孩子，以二叉树的形式呈现。插入后小于父节点的值，无需变更位置。（我们选择的位置始终是从二叉树每次节点的从左到右，为的是保持为满二叉树的数据结构）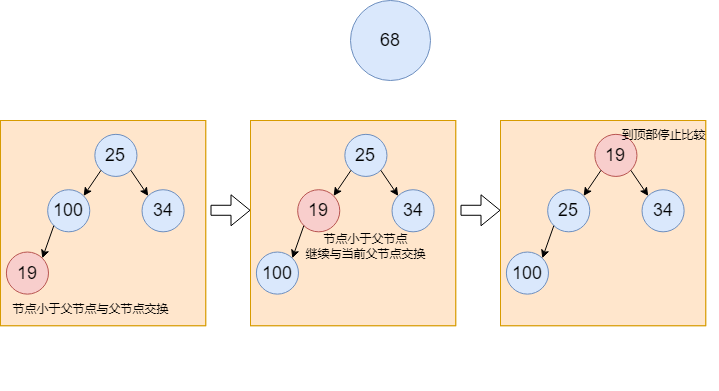

   

5. 元素68继续进入堆中，先成为元素25的右孩子，然后与元素25比较，发现比元素25大，不发生交换，插入完毕后，最终内部的组织顺序如下所示：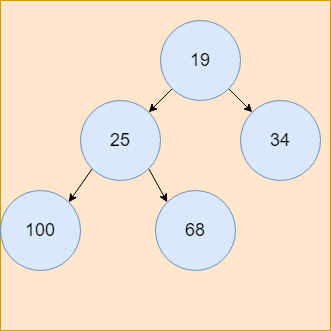

   

6. 下面开始元素出堆的流程的展示，每次出堆，选取的元素都为堆中的顶层节点，获取到顶层节点后，将堆的最后一层的最后一个元素放入到堆顶。最后一个元素放入到堆顶后，需要找到找到该元素的孩子中，较小的元素进行比较，如果比较小的孩子大，则与该孩子交换位置，并继续以上流程以保持最顶上的根节点为最小的元素。以下为交换完后的结构，其中元素25成为新的根节点，元素68下沉到第二层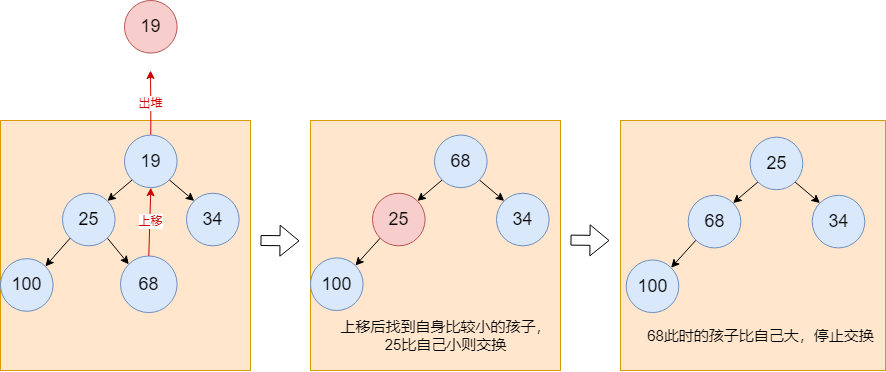

   

7. 元素25继续出堆，并调整堆结构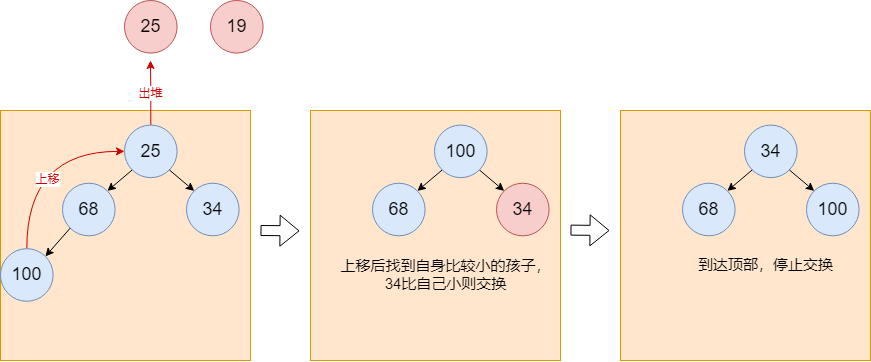

   

8. 元素34继续出堆，并调整堆结构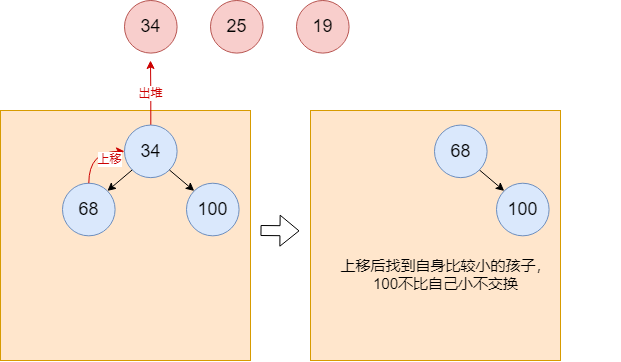

   

9. 元素68继续出堆，并调整堆结构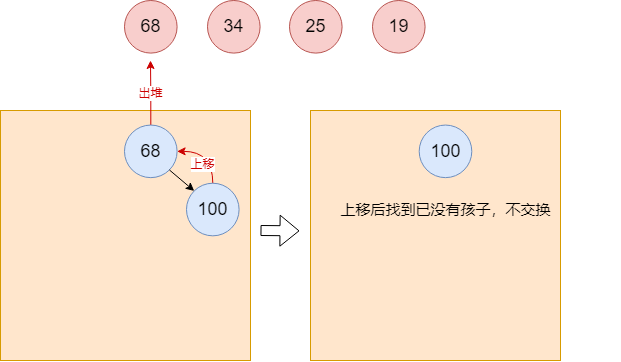

   

10. 最后堆内元素100直接出堆即可，可以得到出小根的先后顺序为由小到小

    

代码实现

实际在代码实现算法的流程的时候，我们用的是数组来代替二叉树的结构，具体的映射关系如下：

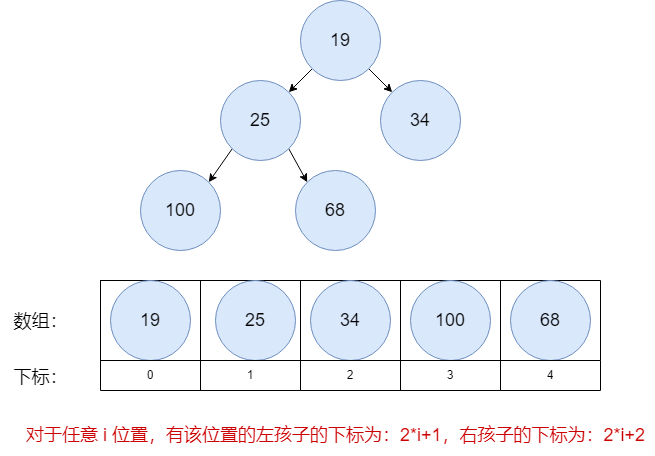
package heap

// 定义的接口类型，方便代码复用
type CanCompareAble interface {
	Less(i, j interface{}) bool
}

// 定义比较规则的函数类型
type LessFunc func(interface{}, interface{}) bool

// 新建一个堆，lessFunc为可选参数，就是比较的规则函数，可以设置为大根堆或者小根堆
func NewHeap(cap int, lessFunc ...LessFunc) *Heap {
	myHeap := &Heap{
		values: make([]CanCompareAble, cap), // 初始化堆的大小，需要能够装下所有的值
		cap: cap,
	}
	if len(lessFunc) > 1 {// 比较函数仅只能设置一个
		panic("堆排序函数超过1个！！！")
	}
	if len(lessFunc) == 1 {
		myHeap.lessFunc = lessFunc[0] // 设置比较规则
	}
	return myHeap
}

type Heap struct {
	values   []CanCompareAble
	index    int
	cap      int
	lessFunc LessFunc
}

func (h *Heap)Empty() bool { // 判断堆是否为空
	return h.index == 0
}

func (h *Heap)Full() bool {  // 判断堆是否满了
	return h.index == h.cap
}

func (h *Heap)Add(value CanCompareAble) { // 进入堆
	if h.Full() {
		panic("over heap size !!!")
	}
	h.values[h.index] = value // 将元素放在最后一层最右边的位置，即数组的可插入的下标
	h.Insert(h.index) //插入后需要向上比较，符合比较规则，则交换位置
	h.index++ //插入下标加1
}

func (h *Heap)Pop() interface{} {  // 出堆
	if h.Empty() {
		panic("heap is empty !!!")
	}
	ans := h.values[0] // 拿到根节点
	h.swap(0, h.index-1) // 将最后一个元素与根节点交换位置
	h.index-- // 插入位置减1
	h.heapify(0) // 节点下沉
	return ans // 返回根节点
}

func (h *Heap) heapify(index int) { // 节点下沉
	leftChild := 2*index + 1  // 找到左孩子
	for leftChild < h.index { // 如果左孩子未越界，则需要比较大小
        // 找到符合规则的那个孩子
		next := leftChild 
		rightChild := leftChild + 1
		if rightChild < h.index && h.IsLess(rightChild, leftChild) {
			next = rightChild
		}
        // 如何满足堆的规则，则与父亲交换
		if h.IsLess(next, index) {
			h.swap(next, index)
		} else {
            // 否则直接停止
			break
		}
        // 继续下沉
		index = next
		leftChild = 2*index + 1
	}
}

func (h *Heap)Insert(index int) {
    // 找到父亲节点
	parent := (index-1)/2
    // 符合堆定义好的规则，则向上交换
	for h.IsLess(index, parent) {
		h.swap(index, parent)
		index = parent
		parent = (index-1)/2
	}
}

func (h *Heap) swap(i, j int) {
	h.values[i], h.values[j] = h.values[j], h.values[i]
}

func (h *Heap)IsLess(i, j int) bool {
	if h.lessFunc != nil {
		return h.lessFunc(h.values[i], h.values[j])
	}
	return h.values[i].Less(h.values[i], h.values[j])
}

调试代码

package heap

import (
	"fmt"
	"testing"
)

type myInt int

func (m myInt) Less(i, j interface{}) bool {
	vi, vj := i.(myInt), j.(myInt)
	return vi < vj
}

func MyLess(i, j interface{}) bool {
	vi, vj := i.(myInt), j.(myInt)
	return vi > vj
}

func TestHeap(t *testing.T) {
	myh := NewHeap(10) // 默认小根堆
	//myh := NewHeap(10, MyLess) // 修改比较参数为大根堆
	myh.Add(myInt(18))
	myh.Add(myInt(15))
	myh.Add(myInt(8))
	myh.Add(myInt(4))
	myh.Add(myInt(3))
	myh.Add(myInt(1))
	fmt.Println(myh.Pop())
	fmt.Println(myh.Pop())
	fmt.Println(myh.Pop())
	fmt.Println(myh.Pop())
	fmt.Println(myh.Pop())
	fmt.Println(myh.Pop())
}

定义与运用

在计算机科学中，堆（Heap）是一种特殊的数据结构，它是一种完全二叉树或近似完全二叉树的数组对象。堆具有以下两个主要特点：

1. 堆属性：堆被定义为一个具有堆属性的完全二叉树。堆属性要求父节点的值（或优先级）要么大于等于（最大堆）其子节点的值，要么小于等于（最小堆）其子节点的值。
2. 堆序性：堆序性要求在一个最大堆中，每个父节点的值都大于或等于其子节点的值；而在一个最小堆中，每个父节点的值都小于或等于其子节点的值。

堆的主要应用场景包括：

1. 堆排序：堆排序是一种高效的排序算法，它利用堆的性质进行排序。堆排序首先构建一个最大堆或最小堆，然后不断地从堆顶取出最大（或最小）元素，将其放入已排序的部分，再调整剩余元素，重复这个过程直到所有元素都被排序。
2. 优先级队列：堆可以用作实现优先级队列的数据结构。优先级队列是一种特殊的队列，其中每个元素都有一个相关的优先级。在优先级队列中，具有最高优先级的元素首先被移除。堆可以用来实现优先级队列的操作，例如插入元素和获取最高优先级元素。
3. 图算法中的最短路径和最小生成树：在一些图算法中，堆被用于选择下一个要访问的节点或边。例如，Dijkstra算法使用最小堆来选择最短路径的下一个节点，Prim算法使用最小堆来选择最小生成树的下一个边。