归并排序

我们有一个数组，前半部分有序，后半部分也有序，但是整体无序如：

算法流程

使用归并排序的核心算法流程使上述数组变有序：

1. 使用一个help数组与当前数组等长，用于放置排序后的数字
2. 对比两个有序部分的数字，小的先往help中填充，直到填充满
3. 填充满help后，将help中的数字填回原数组中即可。

变量初始化：

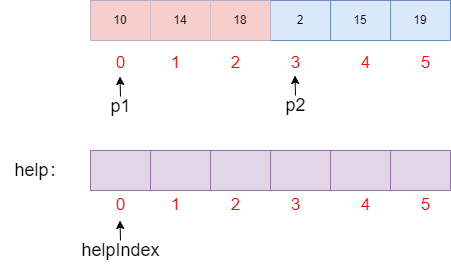
先准备以下四个变量：

• p1 指向前半部分的有序数组的开头位置
• p2 指向后半部分的有序数组的开头位置
• help为辅助数组，用于将两部分的数组重新整理有序
• helpIndex指向当前需要填充数字的位置

算法流程：

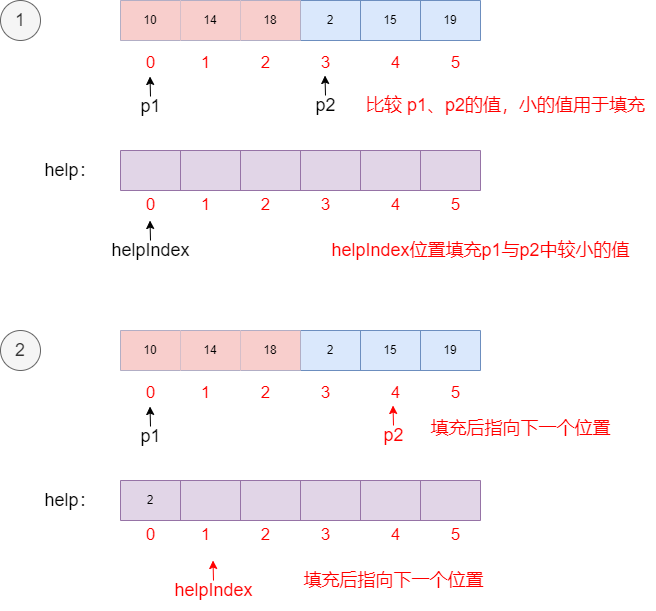
重复上面的步骤①，②，直到help中填充满后，将help数组里有序的值，填回原数组中，数组有序。

实现代码

归并排序，递归与迭代版本

package merge_sort


// 归并排序递归版本，使用递归不断划分区间，使用merge排序
func MergeSortRecursion(arr []int) {
	if len(arr) == 0 {
		return
	}
	MergeSortProcess(arr, 0, len(arr)-1)
}

func MergeSortProcess(arr []int, L, R int)  {
	if L == R { // 区间只有一个数字时停止
		return
	}
	middle := L + ((R-L)>>1)           // 找到中点
	MergeSortProcess(arr, L, middle)   // 左边有序
	MergeSortProcess(arr, middle+1, R) // 右边有序
	merge(arr, L, middle, R)           // 整体有序
}

// 基础merge操作
func merge(arr []int, L, middle, R int) {
	if L == R {
		return
	}
	help := make([]int, R-L+1) // 辅助数组
	helpIndex := 0             // 辅助数组填充位置
	p1 := L                    // 上半部分开始位置
	p2 := middle+1             // 下半部分开始位置
	for p1 <= middle && p2 <= R { // 任何一部分都不越界时来回填入help数组
		if arr[p1] < arr[p2] {
			help[helpIndex] = arr[p1]
			p1++
		} else {
			help[helpIndex] = arr[p2]
			p2++
		}
		helpIndex++
	}
	for p1 <= middle { // 没有填完的继续填写
		help[helpIndex] = arr[p1]
		helpIndex++
		p1++
	}
	for p2 <= R { // 没有填完的继续填写
		help[helpIndex] = arr[p2]
		helpIndex++
		p2++
	}
	// 写回原数组
	for i:=0; i+L <= R; i++ {
		arr[i+L] = help[i]
	}
}


// 归并排序迭代版本
func MergeSortIteration(arr []int) {
	arrLen := len(arr) // 5
	mergeSize := 1     // 1

	for mergeSize < arrLen {  // 1 < 5
		start := 0 // 在mergeSize符合条件的时候，每次从头开始merge
		for start < arrLen { // 找到每个可以merge的开头，进行merge
			// 因长度不均衡，在之前已经merge过了，就不merge了
			if mergeSize >= arrLen - start {
				break
			}

			// 不考虑边界进行计算
			L := start  // 0
			R := L + 2*mergeSize - 1
			middle := L + (R-L)>>1
			// R 存在越界的可能
			R = min(R, arrLen-1)
			merge(arr, L, middle, R)
			start = R + 1
		}

		if mergeSize > arrLen/2 { // 防止越界
			break
		}
		mergeSize <<= 1
	}
}

func min(a, b int) int {
	if a > b {
		return b
	}
	return a
}

测试代码

package merge_sort

import (
	"fmt"
	"goTestToMod/algorithm/utility"
	"goTestToMod/algorithm/utility/arr"
	"testing"
)


func TestRandomSort(t *testing.T) {
	r := utility.GetRandomNumCreator()
	for i:=0; i<10000; i++ { // 大量测试，如果不一致测试用例不通过
		rarr := r.GetRandomArr(100, 10)
		c1 := arr.CopyArr(rarr)
		c2 := arr.CopyArr(rarr)
		MergeSortIteration(c1)  // 使用迭代方式归并排序
		MergeSortRecursion(c2)  // 使用递归方式归并排序
		if !arr.Equal(c1, c2) { // 不相等则代码存在问题
			panic(fmt.Sprintf("【 no equal 】 arr1: %+v, arr2: %+v, originl arr: %+v", c1, c2, rarr))
		}
		if !arr.IsSorted(c1) {  // 排序后还是无序算法有问题
			panic(fmt.Sprintf("【 no sorted 】 after sorted: %+v, originl arr: %+v", c1, rarr))
		}
	}
}

数组随机器

package utility

import (
	"math/rand"
	"time"
)


func GetRandomNumCreator() RandomNumCreator { // 工厂函数，获取我们的随机数生成器
	return RandomNumCreator{
		time.Now().UnixNano(),
	}
}

type RandomNumCreator struct {
	Seed int64
}

func (r *RandomNumCreator) GetRandom(maxNum int) int {
	rand.Seed(r.Seed)
	r.Seed++  // 每次生成随机数改变我们的种子
	return rand.Intn(maxNum)
}

func (r *RandomNumCreator)GetRandomArr(maxNum, maxLen int) []int {
	arrLen := r.GetRandom(maxLen)
	arr := make([]int, arrLen)
	for i:=0 ;i<arrLen; i++ {
		arr[i] = r.GetRandom(maxNum)
	}
	return arr
}

工具包

package arr

func Swap(arr []int, i, j int){
	arr[i], arr[j] = arr[j], arr[i]
}

func CopyArr(arr []int) []int {
	ans := make([]int, len(arr))
	for i, v := range arr {
		ans[i] = v
	}
	return ans
}

func Equal(arr1, arr2 []int) bool {
	if len(arr1) != len(arr2) {
		return false
	}
	for i, v := range arr1 {
		if arr2[i] != v {
			return false
		}
	}
	return true
}

func IsSorted(arr []int) bool {
	if len(arr) == 0 {
		return true
	}
	for i:=1; i<len(arr); i++ {
		if arr[i] < arr[i-1] {
			return false
		}
	}
	return true
}

使用拓展

小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。 例子：

• 1左边比1小的数，没有；
• 3左边比3小的数，1；
• 4左边比4小的数，1、3；
• 2左边比2小的数，1；
• 5左边比5小的数，1、3、4、2；

所以小和为1+1+3+1+1+3+4+2=16

算法流程

以下举一个merge 过程中如何计算小和的流程：

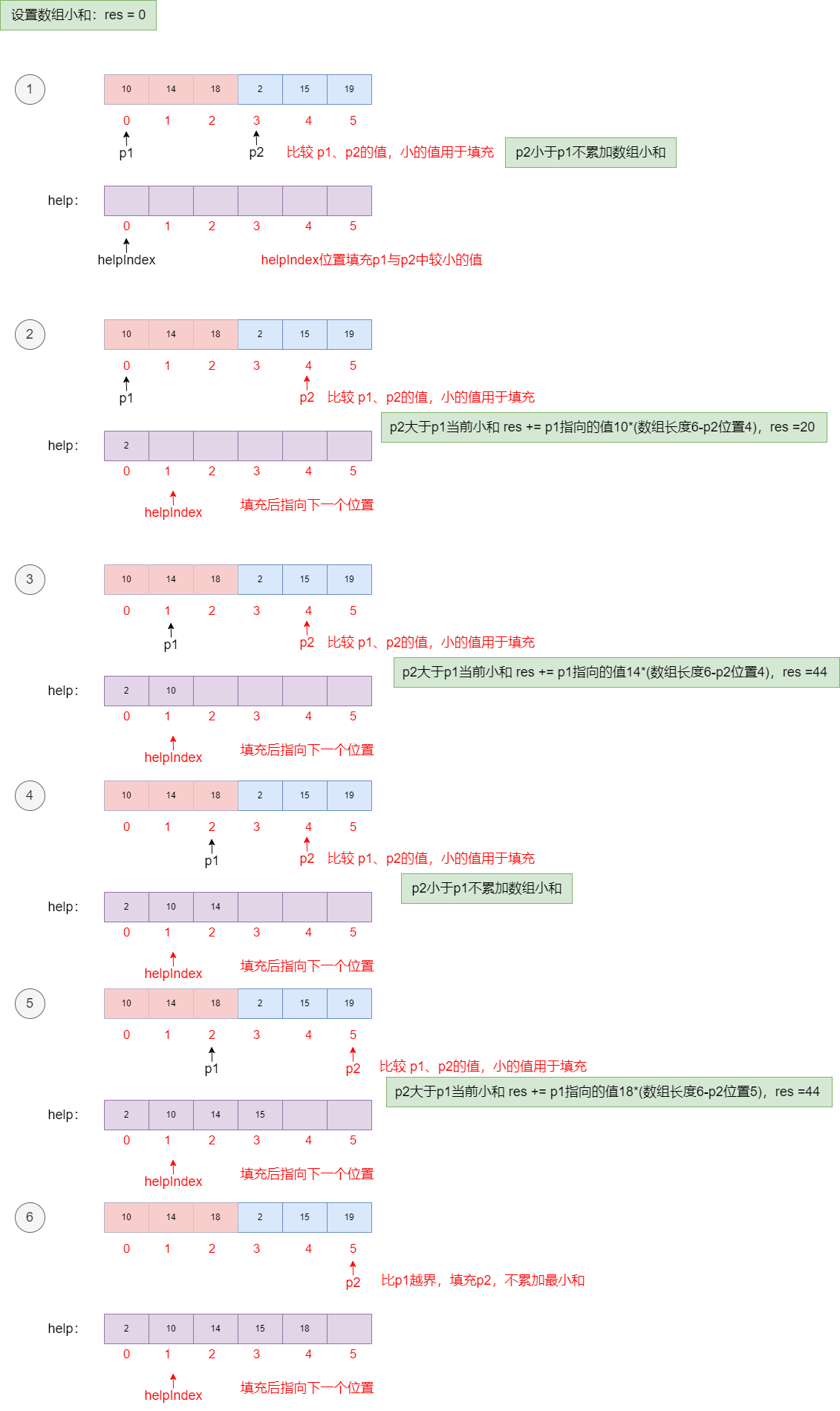
• 以上的方式有一个问题转换，我们正常求小和是遍历当前数之前的数字，如果比当前数字小则累加。在merge过程中我们将问题转换为找当前数字后面有多少个数字比当前数字大，则当前数字需要累加多少次。
• 上述流程是将一次merge的流程计算总和的过程，如果计算整体数组的总和我们可以使用递归将区间不断缩小，最后得出我们整体的小和，参考我们的代码实现。

代码实现

package merge_sort

// merge排序解
func SmallSum(arr []int) int {
	if arr == nil || len(arr) == 0 {
		return 0
	}
	return SmallSumProcess(arr, 0, len(arr)-1)
}

// 将arr l-r 上的范围排序，并且返回最小和
func SmallSumProcess(arr []int, l, r int) int {
	if l == r { // 区间只有一个数的时候没有最小和
		return 0
	}
	mid := l + ((r-l)>>1) // 不懂可以看位运算章节
	return SmallSumProcess(arr, l, mid) +     // 将前面部分排序，并求出最小和
		   SmallSumProcess(arr, mid+1, r) +   // 将后面部分排序并求出最小和
		   SmallSumMerge(arr, l, mid, r)      // 求当前merge时的最小和
}

func SmallSumMerge(arr []int, l, mid, r int) int {
	if l >= r {
		return 0
	}
	help := make([]int, r-l+1) // 初始化help数组
	helpIndex := 0             // help数组下个一填充的位置
	p1, p2 := l, mid+1         // 分别指向前后有序数组的开头
	res    := 0                // 最小和初始为0
	for p1 <= mid && p2 <= r { // 填充help数组
		if arr[p1] < arr[p2] {
			res += arr[p1] * (r - p2 + 1) // 计算小和 = p1中的数*p2中比当前数字大的数量
			help[helpIndex] = arr[p1]
			p1++
		} else { // 相等的情况需要先落p1，且不统计最小和，否则会造成最新小和
			help[helpIndex] = arr[p2]
			p2++
		}
		helpIndex++
	}

	for p1 <= mid {
		help[helpIndex] = arr[p1]
		p1++
		helpIndex++
	}
	for p2 <= r {
		help[helpIndex] = arr[p2]
		p2++
		helpIndex++
	}
	for i:=0; i<len(help); i++ {
		arr[l+i] = help[i]
	}
	return res
}


// 暴力解 O(N^2)
func SmallSumSimple(arr []int) int {
	res := 0
	for i:=0; i<len(arr); i++ {
		for j:=0; j<i; j++ {
			if arr[j] < arr[i] {
				res += arr[j]
			}
		}
	}
	return res
}

测试

func TestSmallSum(t *testing.T) {
	r := utility.GetRandomNumCreator()
	for i:=0; i<50000; i++ { // 大量测试，如果不一致测试用例不通过
		rarr := r.GetRandomArr(1000, 100)
		c1 := arr.CopyArr(rarr)
		c2 := arr.CopyArr(rarr)
		sum1 := SmallSum(c1)  // 使用迭代方式归并排序
		sum2 := SmallSumSimple(c2)  // 使用递归方式归并排序
		if sum1 != sum2{ // 不相等则代码存在问题
			panic(fmt.Sprintf("【 no equal 】 sum1: %+v, sum2: %+v, originl arr: %+v", sum1, sum2, rarr))
		}
	}
}

逆序对问题

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

如输入:

• 以 7 开头的逆序对有三个： (7,5) (7,6) (7,4)
• 以5开头的逆序对有一个：(5,4)
• 以4开头的逆序对有一个：(6,4)

输出总数: 5

算法流程

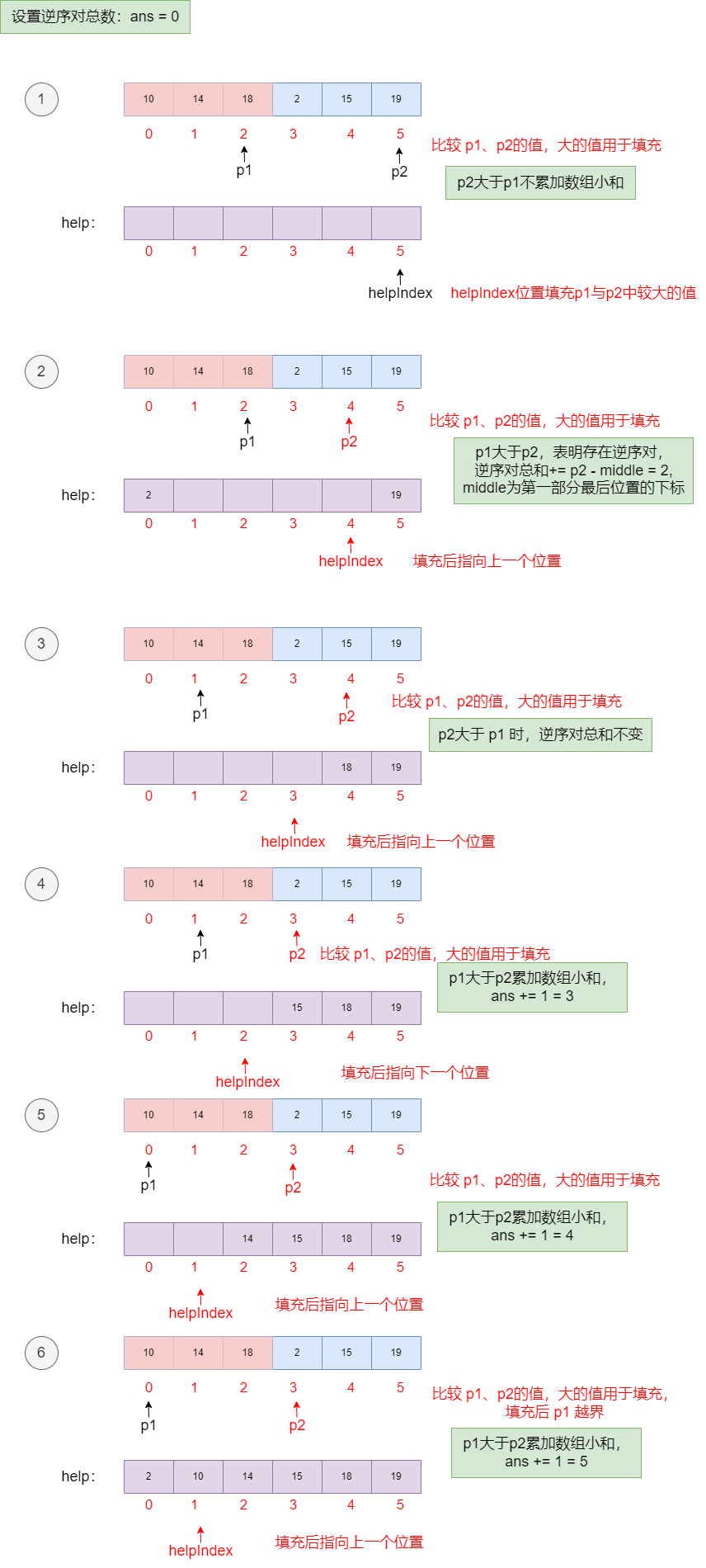
代码实现

leetCode: 交易逆序对的总数 (opens new window)，原题下面代码可以直接跑通

func reversePairs(record []int) int {
	if len(record) <= 1 {
		return 0
	}
	return reversePairsProcess(record, 0, len(record)-1)
}

func reversePairsProcess(record []int, L, R int) int {
	if L == R {
		return 0
	}
	mid := L + (R-L)>>1

	return reversePairsProcess(record, L, mid) +
		   reversePairsProcess(record, mid+1, R) +
		   reversePairsMerge(record, L, mid, R)
}

func reversePairsMerge(arr []int, L, middle, R int) int {
	if L >= R {
		return 0
	}
	ans := 0
	help := make([]int, R-L+1)
	helpIndex := R-L
	p1, p2 := middle, R

	for p1 >= L && p2 >= middle+1 {
		if arr[p1] > arr[p2] {
			help[helpIndex] = arr[p1]
			ans += p2 - middle
			p1--
		} else {
			help[helpIndex] = arr[p2]
			p2--
		}
		helpIndex--
	}

	for p1 >= L {
		help[helpIndex] = arr[p1]
		p1--
		helpIndex--
	}
	for p2 >= middle+1 {
		help[helpIndex] = arr[p2]
		p2--
		helpIndex--
	}
	for i, n := range help {
		arr[L+i] = n
	}
	return ans
}

比右边大两倍的数

找到数组中，所有的数的右边比自身大2倍的数字。同理，不过统计过程不可以服用merge的流程，单拎出来即可。

示例:

func merge(arr []int, l, m, r int) int {
    var ans int
    mr := m + 1
    for i:=0; i<=m; i++ {
        for mr<=r && arr[i] > arr[mr]*2 {
            mr ++ 
        }
        ans += mr - m -1
    }
	// do merge
    return ans
}

区间和的个数

题目连接：区间和的个数 (opens new window)

题目

给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中，值位于范围 [lower, upper] （包含 lower 和 upper）之内的 区间和的个数 。

区间和 S(i, j) 表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。

示例 1：

输入：nums = [-2,5,-1], lower = -2, upper = 2
输出：3
解释：存在三个区间：[0,0]、[2,2] 和 [0,2] ，对应的区间和分别是：-2 、-1 、2 。

示例 2：

输入：nums = [0], lower = 0, upper = 0
输出：1

题解

暴力解法：

• 双重循环，遍历数组每一个开头位置，并找到所有可能结束的位置，在这个区间将总和求出来。
• 如果该区间总和符合要求，统计结果

前缀和数组解法：

假设原数组为：

我们想要知道有多少子区间总和属于[3,5]之间的个数。

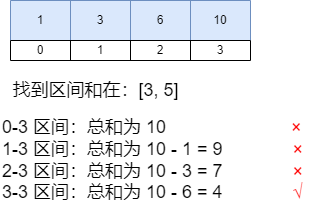
1. 求出前缀和数组，每个i位置为原数组0-i位置数的总和：

   

2. 对于之前的问题，我们可以转化为，找到每一个结尾的位置，并找到以该结尾位置结尾的所有区间符合范围的个数，我们就将该问题解决了。

3. 以前缀和数组中结尾位置作为示例，找到以该位置结尾的子区间有多少个：

   

4. 我们可以再抽象一下：

   

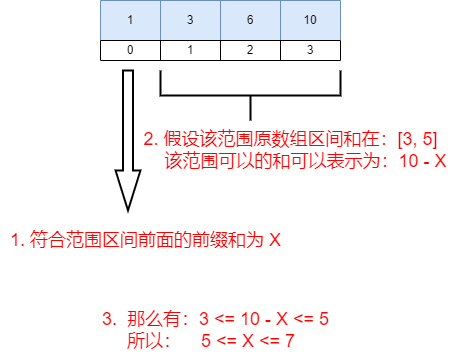
   我们可以得到一个结论：对于 10 这个位置，只要之前有前缀和在 [5, 7]之间，就有对应的10为结束位置的区间在[3, 5]。

5. 对于以任意前缀和为Y的结束位置，该位置任意位置前缀和为X。如果想要存在 以Y为结束位置的范围满足：[low, upper]范围，则需要X满足：[Y-upper, Y- low]这个区间。

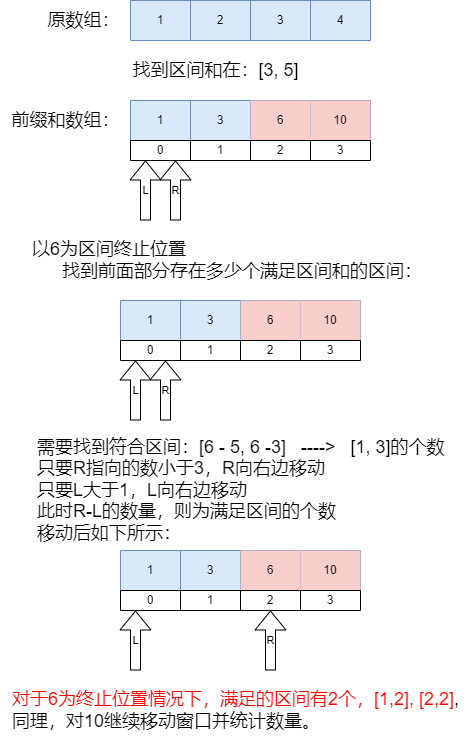
6. 单次merge时，统计满足范围的区间个数：

   

完整题解：

func countRangeSum(nums []int, lower int, upper int) int {
	if nums == nil || len(nums) == 0 {
		return 0
	}
	prefixSum := make([]int, len(nums))
	prefixSum[0] = nums[0]
	for i:=1; i<len(nums);i++ {
		prefixSum[i] = prefixSum[i-1] + nums[i]
	}
	return countRangeSumProcess(prefixSum, 0, len(nums)-1, lower, upper)
}

func countRangeSumProcess(arr []int, l, r, lower, upper int) int {
	if l == r {
		if lower <= arr[l] && arr[l] <= upper {
			return 1
		}
		return 0
	}
	m := l + (r-l)>>1
	return countRangeSumProcess(arr, l, m, lower, upper) +
		   countRangeSumProcess(arr, m+1, r, lower, upper) +
		   countRangeSumMerge(arr, l, m, r, lower, upper)
}

func countRangeSumMerge(arr []int, l, m, r, lower, upper int) int {
	winL, winR := l, l
	ans := 0
	rangeMin, rangeMax := 0, 0
	for i:=m+1; i<=r; i++ {
		rangeMin = arr[i] - upper
		rangeMax = arr[i] - lower
		for winR <= m && arr[winR] <= rangeMax {
			winR++
		}
		for winL <= m && arr[winL] < rangeMin {
			winL++
		}
		ans += winR - winL
	}

	help := make([]int, r-l+1)
	helpIndex := 0
	p1, p2 := l, m+1
	for p1 <= m && p2 <= r {
		if arr[p1] < arr[p2] {
			help[helpIndex] = arr[p1]
			p1++
		} else {
			help[helpIndex] = arr[p2]
			p2++
		}
		helpIndex++
	}
	for p1 <= m {
		help[helpIndex] = arr[p1]
		p1++
		helpIndex++
	}
	for p2 <= r {
		help[helpIndex] = arr[p2]
		p2++
		helpIndex++
	}
	for i:=0; i<len(help); i++ {
		arr[i+l] = help[i]
	}
	return ans
}

本质应用

需要找到数组中前后大小关系满足特殊要求的数量的情况下，都可以使用merge的流程来解决问题。

时间复杂度：O(N*LogN)

空间复杂度：O(N)