图的拓扑排序算法

1. 在图中找到所有入度为0的点输出
2. 把所有入度为0的点在图中删掉，继续找入度为0的点输出，周而复始
3. 图的所有点都被删除后，依次输出的顺序就是拓扑排序

要求：有向图且其中没有环

应用：事件安排，编译顺序

算法示例

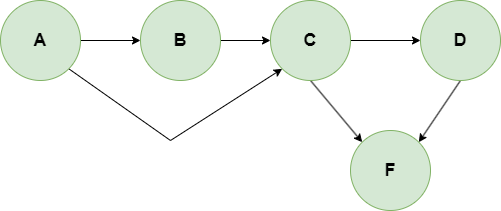
拓扑排序输出顺序： A -> B -> C -> D -> F

• 先找到入度为0的点A,输出并删除点A
• 此时点B的入度为0,输出点B，并删除点B
• 以此类推，依次将结果输出

图的方向可以理解为依赖关系，比如：为什么先输出点B再输出点C？

依照图中，可以理解为，点c输出需要具备 点A与点B都已经输出后，才具备输出条件。

常用场景

• 做事情的有先后顺序且需要具备条件的情况

• 代码编译

  

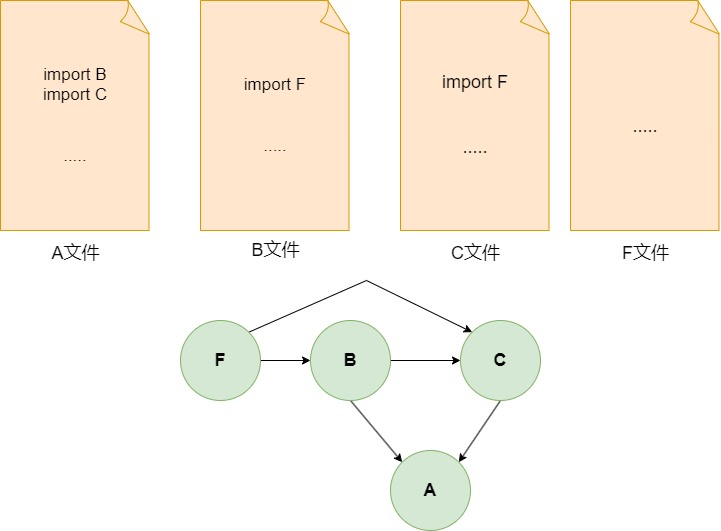
代码

func TopologicalSort(graph Graph) []int {
	// 结果数组
	ans := []int{}
	// 记录节点的入度的map
	nodeInMap := map[*Node]int{}
	// 入度为0的节点才可以进入队列
	zeroInQueue := list.New()
	// 遍历图中，点集，并将入度为0的点放入队列
	for _, v := range graph.Nodes {
		nodeInMap[v] = v.In
		if v.In == 0 {
			zeroInQueue.PushBack(v)
		}
	}

	// 入度为0的队列不为空时，结果就没有搜集完毕
	for zeroInQueue.Len() > 0 {
		// 取出入度为0的一个点
		node := zeroInQueue.Remove(zeroInQueue.Front()).(*Node)
		// 加入结果集
		ans = append(ans, node.Val)

		// 消除搜集点的影响，将该点的直接相邻节点的入度减1，如果入度减完后为0，则放入队列
		for _, next := range node.Nexts {
			nodeInMap[next]--
			if nodeInMap[next] == 0 {
				zeroInQueue.PushBack(next)
			}
		}
	}
	return ans
}

测试用例：

func TestTopologicalSort (t *testing.T) {
	chart := [][]int{
		[]int{0, 1, 7}, // 第一个位置表示权重，
		[]int{0, 2, 1}, // 第二个位置表示出发点的值
		[]int{0, 2, 4}, // 第三个位置表示抵达点的值
		[]int{0, 3, 6},
		[]int{0, 3, 7},
		[]int{0, 4, 5},
		[]int{0, 4, 6},
	}
	graph := GenerateGraph(chart) // 转换函数参考图基础
	fmt.Println(TopologicalSort(graph))
}