🌳 前缀树🌐

前缀树（Trie） 是一种专门为字符串集合设计的树形数据结构。它以其独特的结构和强大的功能，在编程森林中独领风骚。

功能：

1. 🧐 高效存储字符串集合：

   • 前缀树能够高效地存储大量的字符串，以树的形式展现每个字符串的前缀。
   • 每个节点代表字符串的一个字符，从根节点到某个节点的路径表示一个字符串。

2. 🚀 快速查找和插入：

   • 通过前缀树，我们可以快速查找某个字符串是否存在于集合中，而不需要遍历整个集合。
   • 插入新字符串也是高效的，只需沿着树一步步扩展即可。

3. 🔄 前缀匹配和搜索提示：

   • 前缀树的一个显著特点是支持高效的前缀匹配。可以轻松找到所有以某个前缀开头的字符串。
   • 这使得前缀树在搜索引擎、拼写检查和自动补全等应用中大显身手。

应用：

1. 📚 字典和拼写检查：

   • 前缀树被广泛应用于字典和拼写检查系统中，用于快速检索和纠正拼写错误。

2. 📖 搜索引擎：

   • 在搜索引擎中，前缀树被用于高效地存储和检索大量的网页或文档。

3. 📱 自动补全：

   • 许多文本编辑器和输入框中使用前缀树来实现快速的自动补全功能。

4. 🗃️ 文件系统和路由表：

   • 前缀树在文件系统中被用于实现高效的路径检索，同时在路由表中也有广泛的应用。

在编程的大森林中，前缀树如同一颗神奇的树木，为我们提供了高效而强大的字符串处理能力。无论是文字搜索还是自动补全，前缀树都是编程森林中不可或缺的神奇工具！🌲✨

示例

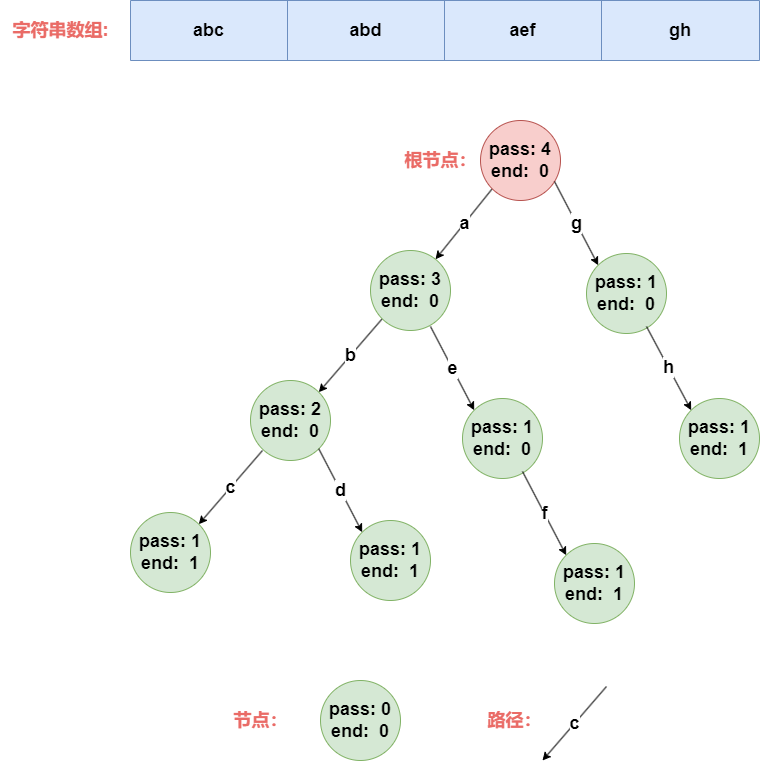
🌳 描绘编程森林：字符串节点树的奇妙构建 🌟

我们能够将数组中的所有字符串巧妙地构建成一颗如上图所示的节点树，其中蕴含着丰富的节点和路径。

节点树的构成：

• pass 属性：标记当前路径上经过的字符串数量。
• end 属性：标记以当前路径结尾的字符串数量。
• 路径：即字符串的每一个字符，逐一构成树的路径。

通过这样的树构建，我们能够迅速回答以下问题：

• 字符是否在数组中出现过？

  • 通过检查树中是否存在当前字符串的路径，若节点的 end 不等于0，则表示字符出现过。

• 出现了几次？

  • 仍然在树中查看当前字符串的路径，此时节点的 end 属性的数量就是字符出现的次数。

• 某一段字符串前缀出现过多少次？

  • 查看树是否包含该字符串前缀，若存在，则通过节点的 pass 属性得知该字符串前缀的出现次数。

代码实现

使用示例

package trietree

import (
	"fmt"
	"testing"
)

func TestTrie(t *testing.T) {
	trieTree := NewTrieTree()
	trieTree.Insert("abc")
	trieTree.Insert("abcd")
	trieTree.Insert("abcde")
	trieTree.Insert("abcdef")
	trieTree.Insert("abcdefg")
	fmt.Println(trieTree.Search("abc"))
	trieTree.Delete("abc")
	fmt.Println(trieTree.Search("abc"))
	fmt.Println(trieTree.Prefix("abcdef"))
}

具体实现

package trietree

func NewTrieTree() *TrieTree {
	// 仅用于英文
	return &TrieTree{root: &Node{pass:0, end:0, next: make([]*Node, 26)}}
}

type TrieTree struct {
	root *Node
}

type Node struct {
	pass int
	end int
	next []*Node
	// next map[string]*Node 数据比较复杂的时候，使用该结构
}

func (t *TrieTree) Insert(str string) {
	if str == "" {  // 防止空字符进入
		return
	}
	cur := t.root  // 从根节点出发
	cur.pass++     // 加入的字符一定不为空，根节点经过的路径一定加一
	var path int   // 表示路径
	for _, v := range str { // 遍历路径
		path = int(v-'a') // 计算实际的路径
		if cur.next[path] == nil { // 不存在路径则创建节点
			cur.next[path] = &Node{pass:0, end:0, next: make([]*Node, 26)}
		}
		cur = cur.next[path] // 走过当前路径
		cur.pass++           // 走过的路径的pass+1
	}
	cur.end++
}

func (t *TrieTree) Search(str string) int {
	cur := t.root // 从根节点出发
	for _, v := range str {
		if cur.next[v-'a'] == nil { // 不存在路径时直接返回 0 个
			return 0
		}
		cur = cur.next[v-'a']
	}
	return cur.end // 返回经过路径的结束数量
}

func (t *TrieTree) Delete(str string) {
	if t.Search(str) != 0 { // 存在该节点时才需要删除
		cur := t.root
		for _, v := range str {
			if cur.next[v-'a'].pass == 1 { // 该路径后续之后唯一一条路径时，直接将整条路径删除, 并返回
				cur.next[v-'a'] = nil
				return
			}
			cur = cur.next[v-'a']
			cur.pass--
		}
		cur.end--
	}
}

func (t *TrieTree) Prefix(str string) int {
	if str == "" {
		return 0
	}
	cur := t.root
	for _, v := range str {
		if cur.next[v -'a'] == nil {
			return 0
		}
		cur = cur.next[v -'a']
	}
	return cur.pass
}