慕溪code

# 2.二进制实现加减乘除

# 题目：

要求使用位运算实现加减乘除，实现过程中不允许出现 +， -， *， / 的计算表达式，只能使用位运算。

力扣原题连接 (opens new window)

# 解析：

# 加法思路：

获取进位的值

假设 a ， b 的值如图：

image-20230319114923019

我们观察 a & b 的结果，由于是a，b相同位置都为1的时候取1。

a + b 的话相同位置为1，则当前位置为0，进位为1。

所以我们将 a & b 左移 1位，即可得到 a + b 的进位部分的值。

当前位置的值

image-20230319130210020

我们观察 a ^ b 的结果，由于是a，b相同位置都不同的时候取1。

a + b 的话相同位置如果不同的话，只能是0和1，则保留1。

所以我们将 a ^ b ，即可得到 a + b 的不包含进位的值。

代码

// 递归写法
func Sum(a, b int) int {
    // 当a等于0时，直接返回b
	if a == 0 {
		return b
	}
    // 记录下原来A的值
	cacheA := a
    // 求出进位的值
	a = (a & b ) << 1
    // 求出不包含即为的值
	b ^= cacheA
    // 继续求和，让进位位一直左移，直到变成0，得到结果返回
	return Sum(a, b)
}

// 非递归写法
func Sum2(a, b int) int {
	var cacheA int
	for a != 0 {
		cacheA = a
		a = (a & b ) << 1
		b ^= mid
	}
	return b
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 减法思路：

我们直到 a - b 等价于 a + （-b），那在计算机中，我们怎么表达取相反数呢？我们先使用 1.int类型的二进制码 打印一下1的二进制表达：

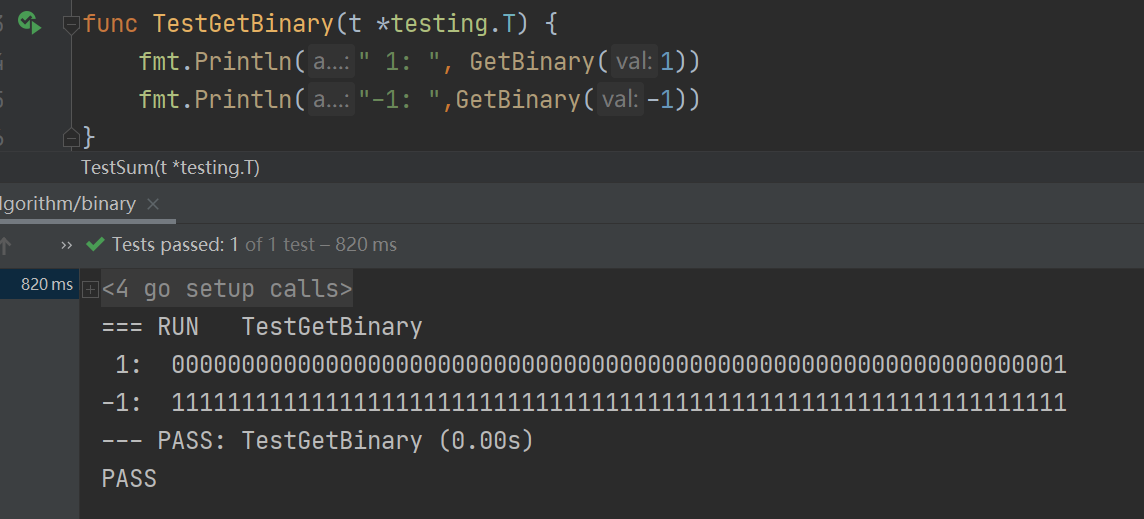
image-20230319150309017

我们发现：-1 的二进制码 等于 1取反加1。

其实在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。好处时可以加快计算机。想要直到具体的原理可以参考补码究竟是什么？ (opens new window)。

所以我们可以使用我们之前实现的加法函数，实现减法：

func Reduce(a, b int) int {
	return Sum(a, Invert(b))
}

// 取反
func Invert(num int) int {
    return Sum2(^num, 1)
}
1
2
3
4
5
6
7
8

测试 10 - 5：

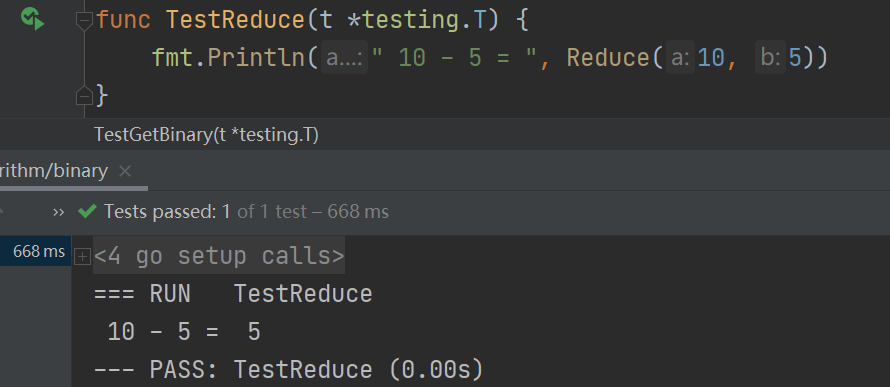
image-20230319154022242

# 乘法思路：

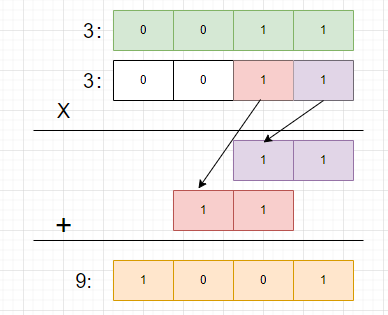
image-20230319202802840

上图给出了 3 * 3 二进制乘法的具体的示例，我们采用乘法竖式，可以得出每位相乘的结果，最后累加，即刻得出答案9的二进制。

我们想达到与乘法竖式相同的结果可以使用如下的方式：

  1. 初始化 答案 Ans 等于0，被乘数左移0位，乘数与1左移0位相与不等于0，则根据乘法竖式，Ans需要加上此时的左移0位的被乘数3.

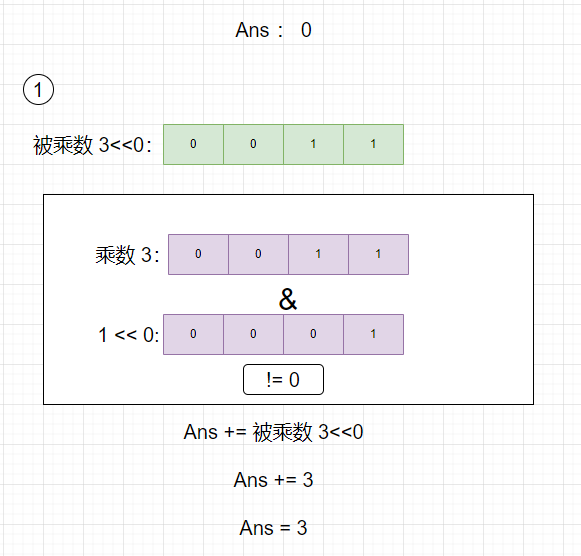
image-20230319210126168

  1. 被乘数左移1位，乘数与1左移1位相与不等于0，则根据乘法竖式，Ans需要加上此时的左移1位的被乘数3.

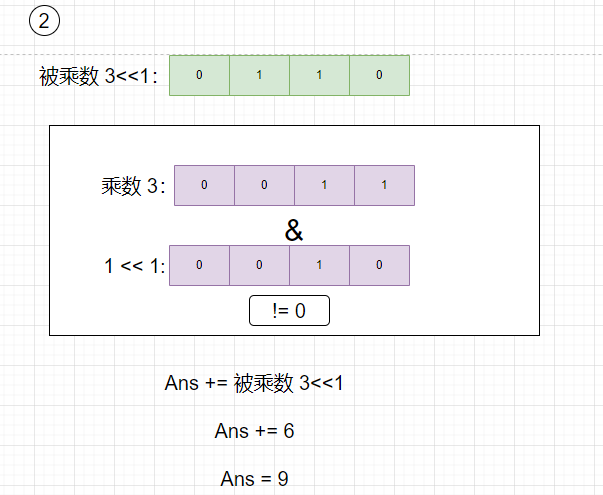
image-20230319220818107

  1. 被乘数左移2位，乘数与1左移2位相与不等于0，则根据乘法竖式，Ans需要加上此时的左移2位的被乘数6.

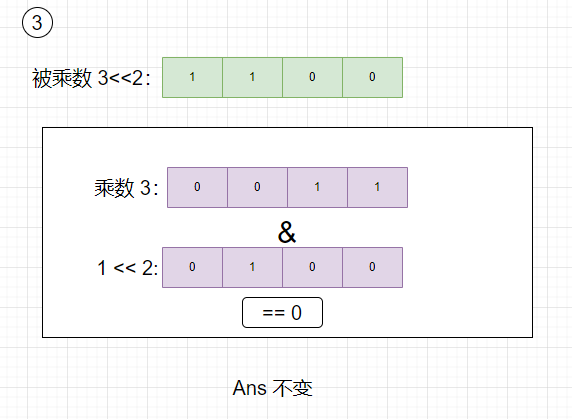
image-20230319220935861

  1. 被乘数左移3位，乘数与1左移3位相与等于0，则根据乘法竖式，Ans需要加上0，Ans不变

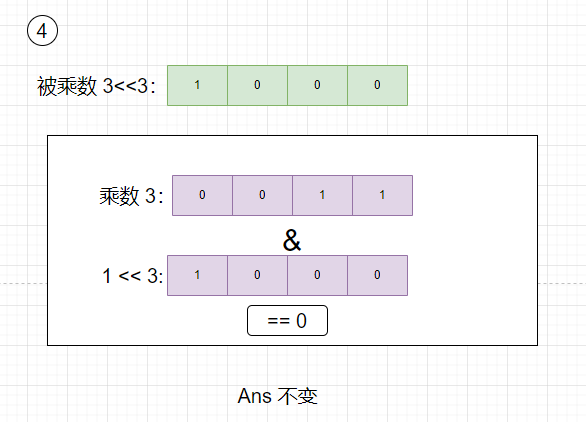
image-20230319221045130

得出Ans = 9. 以上以4位的二进制的正数作为例子，实际实现乘法的时候，需要考虑正负数。

通过观察其实，只要保证乘数左移的时候不将符号数左移即可，java中有无符号左移，所以在java中无需特殊处理，但是由于在go中没有无符号左移，所以在go中，如果乘数是负数，需要将乘数取反进行计算，最后的时候还原符号返回即可。

代码

// 递归版本
func MultiplyProcess(a, b, ans int) int {
	// 当乘数为0时，则已经获取到了所有的累加和
	if b == 0 {
		return ans
	}
	// 如果b小于0，需要取反进行计算
	bLessZero := false
	if b < 0 {
		bLessZero = true
		b = Invert(b)
	}
	// 当前位置不等于0，累加结果
	if b & 1 != 0 {
		ans = Sum2(ans, a)
	}
	// 被乘数左移
	a <<= 1
	// 乘数右移
	b >>= 1
	// 恢复计算现场
	if bLessZero {
		b = Invert(b)
		ans = Invert(ans)
	}
	return MultiplyProcess(a, b, ans)
}


// 迭代版本
func Multiply2(a, b int) int {
	bLessZero := false
	if b < 0 {
		bLessZero = true
		b = Invert(b)
	}
	ans := 0
	for b != 0 {
		if b & 1 != 0 {
			ans += a
		}
		a <<= 1
		b >>= 1
	}
	if bLessZero {
		return Invert(ans)
	}
	return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 除法思路：

采用除法竖式的思路，我们一步一步的确定我们结果每一个位置上是去0还是取1，通过移位并对比做减法，我们可以得到除法的答案，具体步骤如下：

image-20230320001554457

我们以 4位的二进制除法 做了我们的例子，同过上述思路我们，可以初步确定我们的代码逻辑，但是还需要注意，在除法中，我们需要比较两数大小，如果带上符号位，在有正负的情况下我们不好做对比，所以我们可以将两个数都转为正数，最后根据原来的值决定是否需要修改符号返回。

由于负数在二进制总比表达正数的数多一个如二位的二进制：00->[0] ，01->[1] ，10->[-2] ，11->[-1] 。我们还需要注意一下几种情况，如：-2 / -1 原则上 -2/-1 等于 2，但是由于我们的最大值是1，我们无法有2这个值。我们还认为最小值除以-1等于最大值，所以我们认为在这种情况下 -2/-1 = 1

另一种情况：假设我们现在只有三位二进制数，0000 -> 1111 ，则我们能表示的数字是 -8 -> 7 之间的数，此时 -8/2 = -4，由于我们算除法的时候，需要对 -8 -> [1000] 取反加1 变成 [0111] -> 7 ，此时 7/2 = 3，与预期少了1。

所以，在被除数为最小的时候，如：-8 / 2 的时候，我们使用 (-8 + 1)/2 得到 -3，我们将 -3 * 2 = -6，此时 -8 - （-6 ）= -2，用 -2 / 2 = -1，此时将差值 -1 + (-3) = -4，此时可以得到正确结果。

我们通过图示的方式可以计算出结果，但是有特殊情况如下：

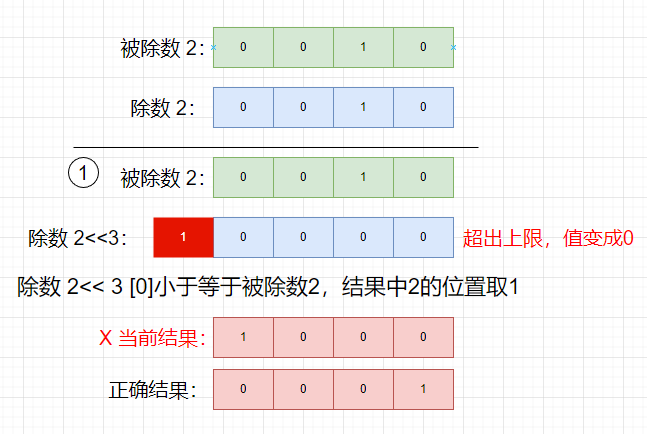
image-20230322000641279

我们发现，使用除数左移，容易超出上限，导致得到错误的结果。

所以我们实际使用被除数左移，从上限移动到0位。

image-20230322001200312

代码

func divide(dividend int, divisor int) int {
	if divisor == math.MinInt32 && dividend == math.MinInt32 { 
        // 为什么是 math.MinInt32 为最小值？因为力扣采用的是int32做的测试用例
        // 最小值除本身等于 1
		return 1
	} else if divisor == math.MinInt32 {
        // divisor 为系统最小时 除了相等的时候都是0
		return 0
	} else if dividend == math.MinInt32 {
		if divisor == Invert(1) {
			return math.MaxInt32
		}
		ans := Div2(dividend, divisor)
		return Sum2(ans, Div2(Reduce(dividend, Multiply2(ans, divisor)), divisor))
	}
	return Div2(dividend, divisor)
}


func Div2(a, b int) int {
	isALessZero, isBLessZero := false, false
	if a < 0 {
		isALessZero = true
		a = Invert(a)
	}
	if b < 0 {
		isBLessZero = true
		b = Invert(b)
	}
	ans := 0
	for i:=62; i>=0; i-- {
        // 采用 a 右移 i 位
		if (a >> i) >= b {
			ans |= 1<<i
			a = Reduce(a, b<<i)
		}
	}
	if isALessZero && isBLessZero {
		return ans
	} else if isALessZero || isBLessZero {
		return Invert(ans)
	}
	return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# 完整代码：

可拷贝到力扣网站直接执行通过，已验证。力扣原题连接 (opens new window)

import "math"

func Sum(a, b int) int {
	if a == 0 {
		return b
	}
	cache := a
	a = (a & b ) << 1
	b ^= cache
	return Sum(a, b)
}

func Sum2(a, b int) int {
	var mid int
	for a != 0 {
		mid = a
		a = (a & b ) << 1
		b ^= mid
	}
	return b
}

func Reduce(a, b int) int {
	return Sum(a, Invert(b))
}

func Invert(num int) int {
	return Sum2(^num, 1)
}

func MultiplyProcess(a, b, ans int) int {
	// 当乘数为0时，则已经获取到了所有的累加和
	if b == 0 {
		return ans
	}
	// 如果b小于0，需要取反进行计算
	bLessZero := false
	if b < 0 {
		bLessZero = true
		b = Invert(b)
	}
	// 当前位置不等于0，累加结果
	if b & 1 != 0 {
		ans = Sum2(ans, a)
	}
	// 被乘数左移
	a <<= 1
	// 乘数右移
	b >>= 1
	// 恢复计算现场
	if bLessZero {
		b = Invert(b)
		ans = Invert(ans)
	}
	return MultiplyProcess(a, b, ans)
}

func Multiply2(a, b int) int {
	bLessZero := false
	if b < 0 {
		bLessZero = true
		b = Invert(b)
	}
	ans := 0
	for b != 0 {
		if b & 1 != 0 {
			ans += a
		}
		a <<= 1
		b >>= 1
	}
	if bLessZero {
		return Invert(ans)
	}
	return ans
}

func divide(dividend int, divisor int) int {
	if divisor == math.MinInt32 && dividend == math.MinInt32 {
		return 1
	} else if divisor == math.MinInt32{
		return 0
	} else if dividend == math.MinInt32 {
		if divisor == Invert(1) {
			return math.MaxInt32
		}
		ans := Div2(dividend, divisor)
		return Sum2(ans, Div2(Reduce(dividend, Multiply2(ans, divisor)), divisor))
	}
	return Div2(dividend, divisor)
}


func Div2(a, b int) int {
	isALessZero, isBLessZero := false, false
	if a < 0 {
		isALessZero = true
		a = Invert(a)
	}
	if b < 0 {
		isBLessZero = true
		b = Invert(b)
	}
	ans := 0
	for i:=62; i>=0; i-- {
		if (a >> i) >= b {
			ans |= 1<<i
			a = Reduce(a, b<<i)
		}
	}
	if isALessZero && isBLessZero {
		return ans
	} else if isALessZero || isBLessZero {
		return Invert(ans)
	}
	return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
上次更新: 10/2/2023,

← 位运算-4-位图 →