# 最小生成树Kruskal
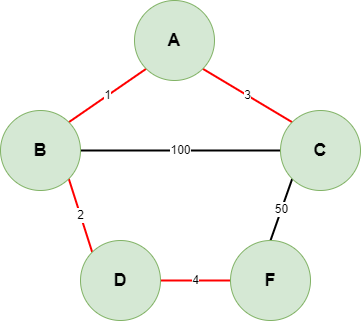
有向图与无向图,都可以使用最小生成树的算法,以下使用无向图做示例
最小生成树问题就是:
- 以最小的代价将图中的节点都联通,求出此时的权重,或者联通节点的边的集合。
- 或者说是再不破坏联通性的条件下,可以删除一些多余的边,保证删除多余的边后,权重最小。
# 算法流程
将边按权重从小到大排序
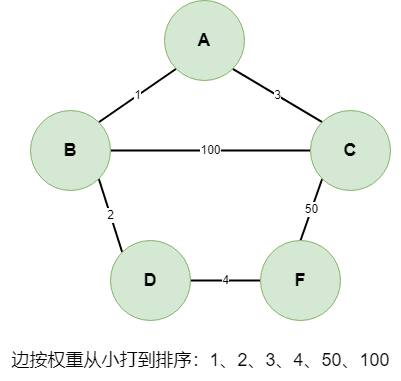
从小到大遍历每条边,并判断边的两边的点是否已经连通,如果未连通则选择该边加入结果集,如果已经连通则放弃该边。
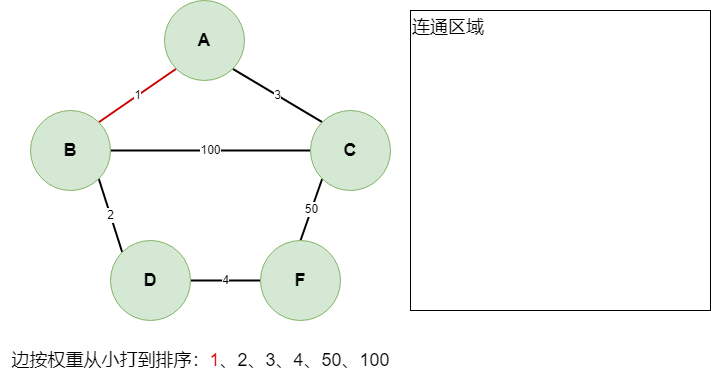
遍历最小权值边1时,两边的
A点与B点此时并未连通,所以选择该边,此时A点与B点连通,加入连通区,边1加入结果集,如下: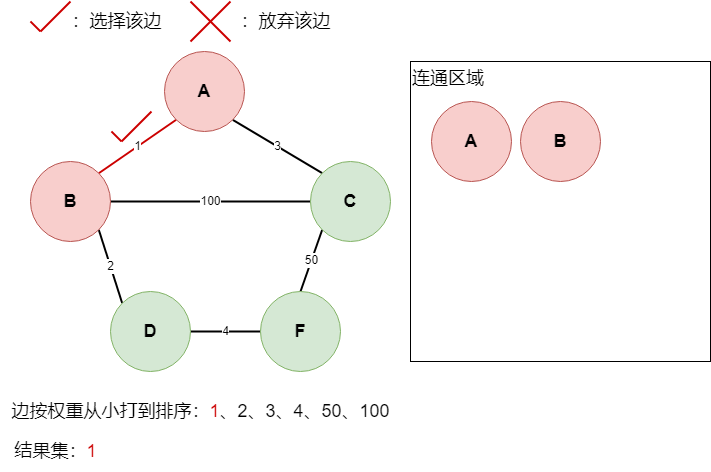
继续遍历下一小的边,并判断,边两头的点是否连通,如果未连通则选择该边加入结果集,如果已经连通则放弃该边。
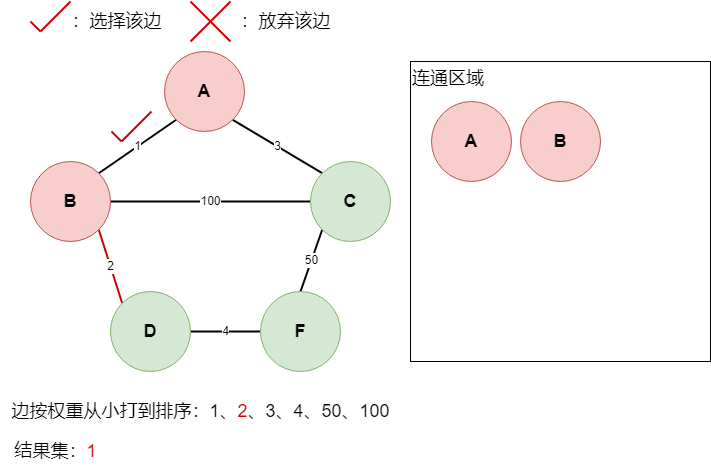
此时遍历到边2时,两边的
B点与D点此时并未连通,所以选择该边,此时B点与D点连通,加入连通区,边2加入结果集如下: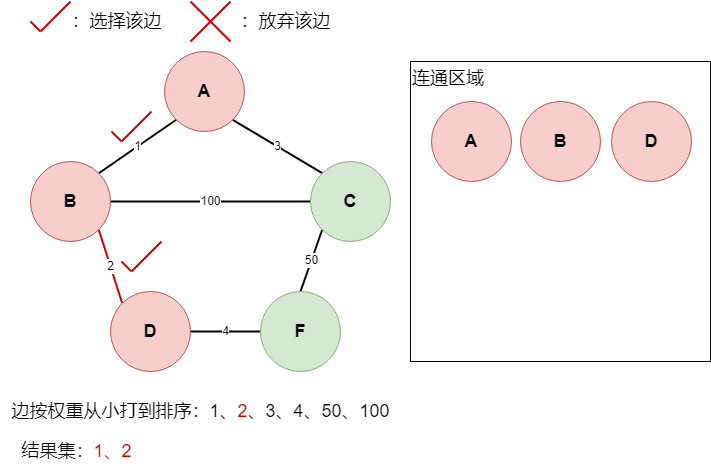
边3与边4遍历过程重复以上操作,可以得到如下图所示:
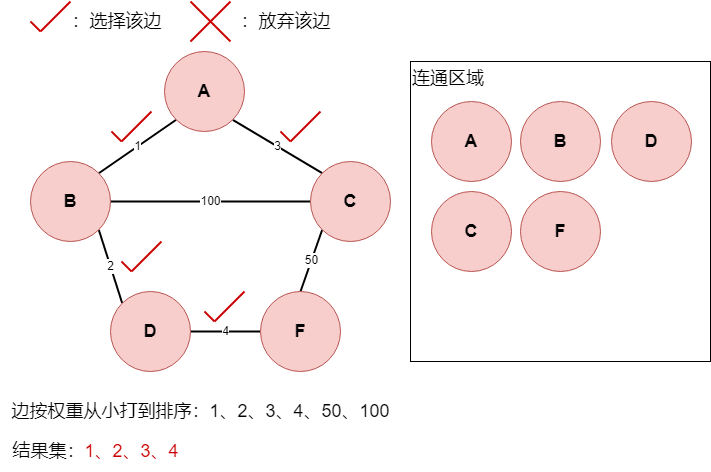
继续遍历,遍历到
边50,此时,C点与F点,已经有由边3,边1,边2,边4连通在一起,所以放弃边50,结果集不变。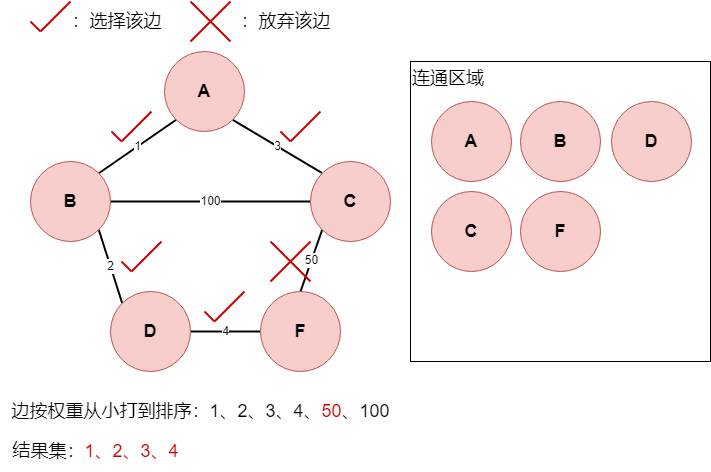
继续遍历,遍历到
边100,此时,C点与B点,已经有由边3,边1连通在一起,所以放弃边100,结果集不变。自此,我们遍历完所有的边,收集到结果集,最小权重即为结果集的边的权重相加。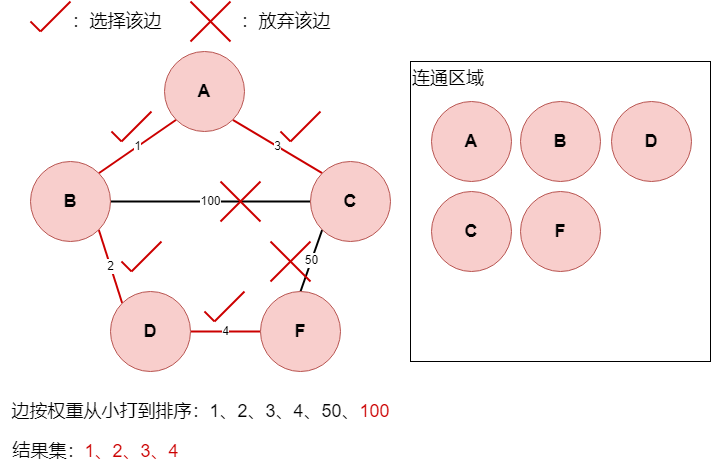
# 代码实现
/*
并查集与堆的实现,需要参考对应章节。
*/
func KruskalMinSum(graph Graph) int {
// 初始化结果权重
var ans int
// 获取所有的点,使用点创建并查集
nodeArr := []interface{}{}
for _, node := range graph.Nodes {
nodeArr = append(nodeArr, node)
}
// 初始化并查集,用于判断两点是否连通
nodeUnionSet := union_set.NewUnionSet(nodeArr)
// 创建小根堆,使遍历的边有序
smallHeap := heap.NewSmallHeap(len(graph.Edges))
for edge, _ := range graph.Edges {
smallHeap.Push(edge)
}
// 从小到大遍历所有的边
for smallHeap.Size() > 0 {
edge := smallHeap.Pop().(*Edge)
if !nodeUnionSet.IsSameSet(edge.From, edge.To) {
// 如果边两头的点不在同一个集合,选择该边,加上该边的权重
ans += edge.Weight
// 选择边后,需要将两个点连通
nodeUnionSet.Union(edge.From, edge.To)
}
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
← 图-2-图的拓扑排序 堆-1-堆及应用 →