计数排序

🔢 编程世界的算法宝典：计数排序 🌐

背景：

计数排序是一种非比较排序算法，它的核心思想是通过统计每个元素的个数，然后根据这些统计信息将元素放回原数组中。虽然它在某些情况下的应用受到限制，但在特定场景下，它展现出了强大的性能。

场景与优势

使用场景：

1. 📊 整数排序：

   • 计数排序最适用于排序整数或具有确定范围的整数集合。它的性能在这种情况下较为出色，尤其是当整数范围相对较小而且分布均匀时。

2. 🎲 稀疏整数集合排序：

   • 如果输入序列中有许多重复的元素，计数排序能够高效地处理，因为它通过计数可以直接确定元素的最终位置。

3. 📁 外部排序辅助：

   • 在外部排序中，当内存有限但元素分布较为均匀时，计数排序可以作为辅助排序算法，提高整体排序性能。

优势：

1. ⏳ 线性时间复杂度：

   • 计数排序的时间复杂度为O(n+k)，其中n是元素个数，k是元素范围。在某些情况下，它的性能超越了比较排序算法。

2. 🛢️ 非比较排序：

   • 与快速排序、归并排序等比较排序算法不同，计数排序不涉及元素之间的比较，而是通过计数统计直接确定元素的位置。

3. 🧩 适用范围广：

   • 计数排序对于整数排序和有限范围的元素集合非常适用，尤其在面对这类特殊情况时，它能够发挥出色的排序能力。

在编程的排序领域中，计数排序是一颗璀璨的宝石，虽然不适用于所有场景，但在特定的宝藏中，它闪烁着独特的光芒。🌟✨

案例展示

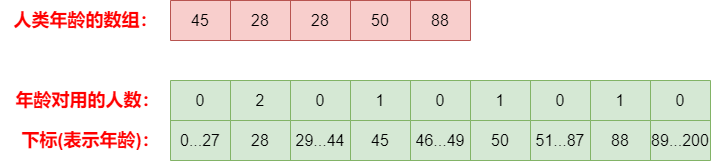
假设我们手中握有一串年龄数组，想要按年龄排序，这时候，我们可以施展计数排序的神奇魔法。

1. 🧙 召唤统计仪：初始化数组

   首先，我们召唤一把有着200个援兵的数组，其中每个下标代表一个年龄（0-199），而对应的值则是该年龄的人数。这就是我们的统计仪，为年龄人数统计蓄力待发。

2. 🚶‍♂️ 征程启程：遍历援兵数组

   遍历这支援兵队伍，逐个提取年龄信息，然后在统计仪中找到相应位置，将对应年龄的人数加一。统计仪随之不断壮大，记录着每个年龄的伙伴数量。

3. 🏹 年龄填充：重塑原始队伍

   此刻，我们按照年龄的从小到大，依次遍历统计仪。根据仪器的记录，我们将年龄信息有序地填回原始数组。这就像是一个年龄舞会，从小朋友开始，一直跳到长者，整个队伍焕然一新，有序而井然有序。

代码实现

package sort

import (
	"math"
	"traning/algorithm/utility"
)

// 年龄的排序示例
func CountSortByAges(arr []int) {
	help := make([]int, 200)
	for _, v := range arr {
		help[v]++
	}
	index := 0
	for i, v := range help {
		for v > 0 {
			arr[index] = i
			index++
			v--
		}
	}
}

// 适用于非负的数组排序
func CountSort(arr []int){
	if len(arr) < 2 {
		return
	}
	var max int = math.MinInt64
	for _, n := range arr {
		max = utility.Max(max, n)
	}
	var buckets []int = make([]int, max+1)
	for _, n := range arr {
		buckets[n]++
	}
	var index int
	for value, count := range buckets {
		for count > 0 {
			arr[index] = value
			index++
			count--
		}
	}
}