Master公式

认识递归

我们有一个数组，想要获取数组中的最大值，我们使用递归来求数组中的最大值。 🌌

1. 🔄 二分之旅：将问题分为两半

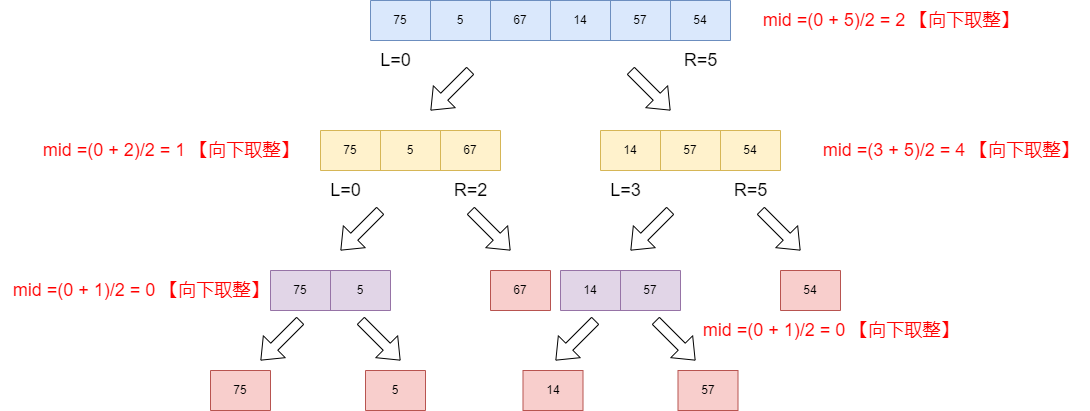
   我们每一次都将求最大值的问题拆分成两个子问题，将数组范围一分为二。然后，比较前半部分的最大值与后半部分的最大值，返回两者中较大的那个值。这就如同在探险的路上，将未知的领域分为两个区域，寻找更大的可能。

2. 🌐 较量之巅：比较两部分的最大值

   在每一步，我们在前半部分和后半部分中找到了各自的最大值，然后进行一场较量之巅，决出两者的胜负。无论是在山巅还是深谷，我们总是希望找到更高更大的存在。

3. 🎯 最终之数：返回当前数字

   如此往复，直到最后范围只有一个数字，我们不再分割，而是毫不犹豫地返回当前数字。这个数字就像是我们探险的最终目标，而它便是整个数组的最大值。

代码示例

func FindMax(arr []int, L, R int) int {
	if L == R {                // 只有一个数字的时候直接返回
		return arr[L]
	}
	mid := L + ((R-L)>>1)      // 求出中点，后面使用了位运算可以参考位运算章节
	return Max(                // 求最大值
		FindMax(arr, L, mid),  // 前半段为 [L, mid]
		FindMax(arr, mid+1,R)) // 前半段为 [mid+1, R]
}

func Max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

master公式

这个公式的神奇之处在于能够帮助我们预测递归算法的时间复杂度。

T(N) = a * T(N/b) + O(N^d)

• 如果 log(b, a) > d，那么递归的复杂度为 O(N^log(b,a))
• 如果 log(b, a) < d，那么递归的复杂度为 O(N^d)
• 如果 log(b, a) = d，那么递归的复杂度为 O(N^d*log(2,N))

数组最大值的时间复杂度

对于我们之前找数组最大值递归的例子，我们可以根据master公式的定义，得到我们算法对应master公式中a,b,d的值。

• 在每层递归中，我们将问题规模减半，即 T(N) = 2 * T(N/2)，并额外执行一次 O(1) 的操作。这使得我们得到：

  • a = 2
  • b = 2
  • d = 0

  因此：

  • log(b, a)(1) > d(0)，因此递归的复杂度为 O(N)

如果我们在之前的基础上在每一次递归对数组做一次遍历呢？

1. 根据公式：

   T(N) = 2 * T(1/2*N) + O(N)
   

   • a = 2
   • b = 2
   • d = 1

2. log(b, a) = 1 = d

3. 时间复杂度为：O(N*log(2,N))

如果我们硬是写代码把问题规模设置为2/3有重复部分，且在每一次递归对数组做一次遍历呢？

1. 写出公式：

   T(N) = 2 * T(2/3*N) + O(N)
   

   • a = 2
   • b = 1.5
   • d = 1

2. log(b, a) > 1 = d

3. 时间复杂度为：O(N^log(b, a))