链表相交系列问题

🧩链表是数据结构中的一种基础且常用的数据类型，它在内存中通过节点的指针链接起来，形成一个动态的数据结构。

链表相交的应用：

链表相交是链表领域中一个引人瞩目的话题，它在算法题中有着许多实际应用。以下是一些链表相交问题的应用场景：

1. 交点检测： 判断两个链表是否相交，如果相交，找到它们的交点。这类问题常常出现在系统设计中，例如交叉路口的监控系统，需要检测不同方向车辆的行驶情况。
2. 环检测： 判断链表中是否存在环，如果存在，找到环的起始点。这类问题与链表相交类似，可以用于检测系统中的资源循环利用或者避免死锁的场景。
3. Y型交叉： 有时两个链表可能在某一点后合并为一个链表，形成Y型。解决这类问题可以应用于用户行为分析，通过用户的历史行为和当前行为的交叉点推测用户兴趣点。
4. 并发操作： 在并发编程中，链表相交问题也有着一定的应用。例如，多个任务同时操作链表，需要确保线程安全和避免数据竞争。

环形链表 (opens new window)

算法流程

给定一个链表，返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

**说明：**不允许修改给定的链表。

示例 1：

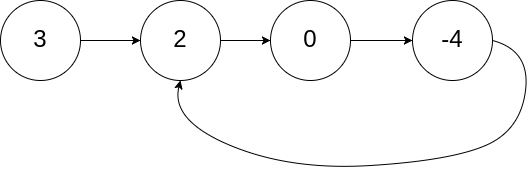
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

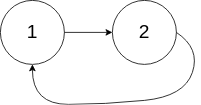
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

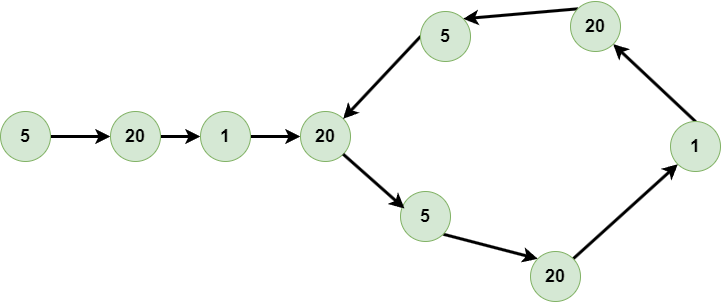
我们有如上这个链表，下面演示算法流程:

代码实现

func detectCycle(head *ListNode) *ListNode {
	if head == nil || head.Next == nil || head.Next.Next == nil {
		return nil
	}
	slow, fast := head.Next, head.Next.Next
	for slow != fast  {
		if fast == nil || fast.Next == nil {
			return nil
		}
		slow = slow.Next
		fast = fast.Next.Next
	}
	slow = head
	for slow != fast {
		slow = slow.Next
		fast = fast.Next
	}
	return slow
}

无环相交链表 (opens new window)

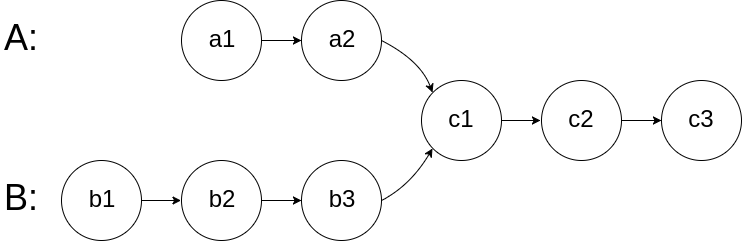
给定两个单链表的头节点 headA 和 headB ，请找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交**：**

(opens new window)

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

(opens new window)

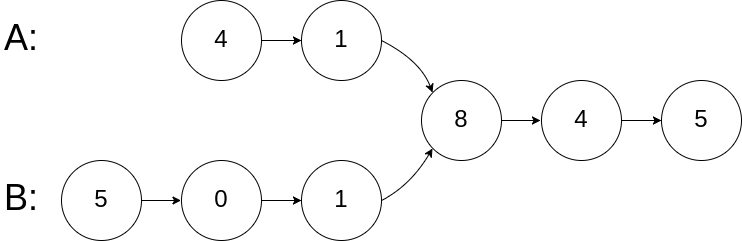
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

(opens new window)

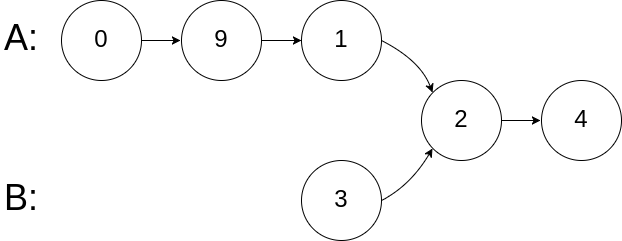
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

(opens new window)

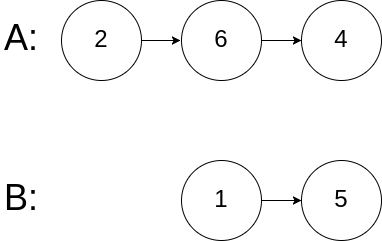
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

算法流程

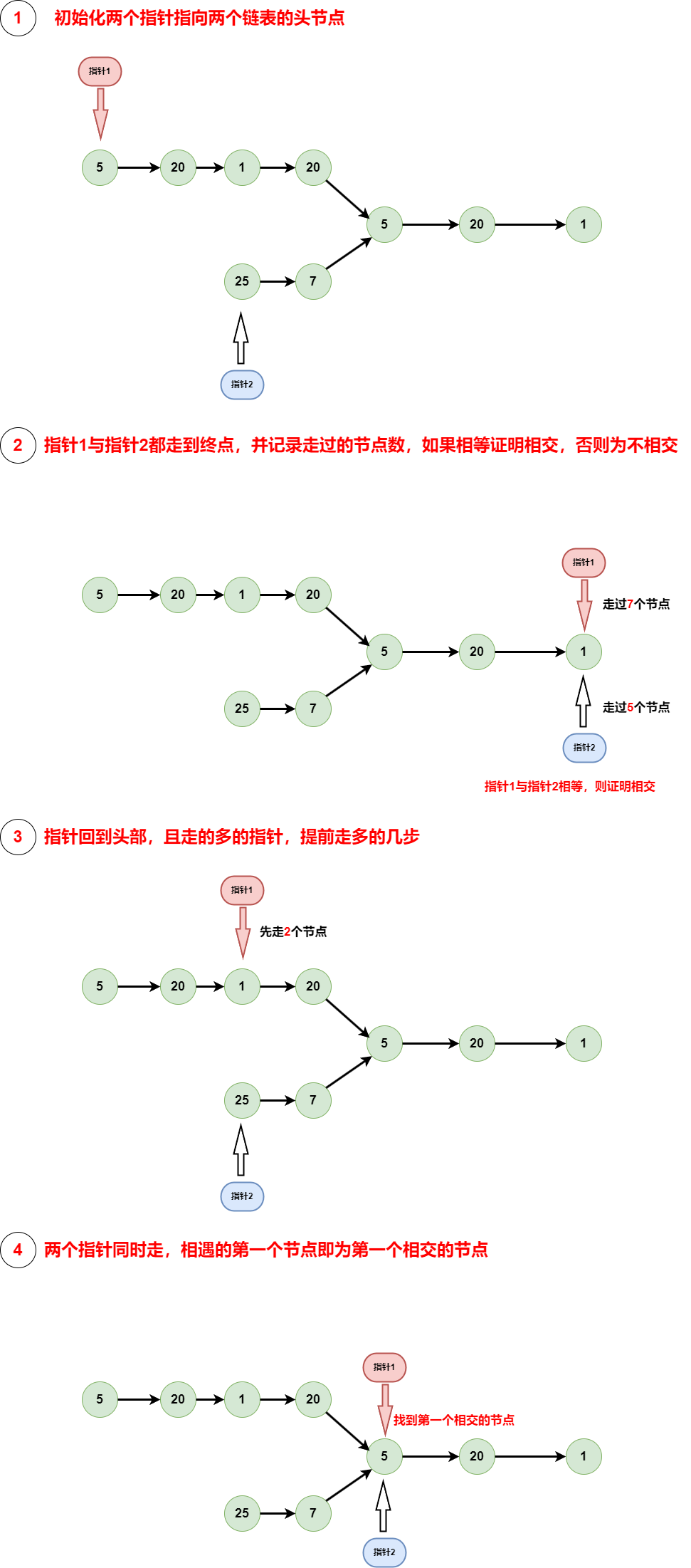
代码实现

func getIntersectionNode(headA, headB *ListNode) *ListNode {
	if headA == nil || headB == nil {
		return nil
	}
	p1, p2 := headA, headB  // 初始两个指针分别指向两个链表的头部
	n := 0                  // 初始化n记录步长
	for p1.Next != nil {
		p1 = p1.Next        // 第一个链表开始走，直到走到最后一个节点
		n++                 // 记录走过的步数
	}
	for p2.Next != nil {
		p2 = p2.Next        // 第二个链表开始走，直到走到最后一个节点
		n--                 // 每走一步第一个指针走过的步数减一，最后得到步数差
	}
	if p1 != p2 {           // p1 p2 不相等则不相交，直接返回nil
		return nil
	}
	p1, p2 = headA, headB   // 回到开头
	if n < 0 {              // 如果n小于0，则p1走的步数小于p2
		p1, p2 = p2, p1     // 调换p1 与 p2，使p1始终指向长一点的链表
	}
	n = abs(n)
	for n != 0 { 			// 长的链表先走步差
		p1 = p1.Next
		n--
	}
	for p1 != p2 {          // 同时走找到第一个相遇的节点，即为第一个相交的节点
		p1 = p1.Next
		p2 = p2.Next
	}
	return p1
}

func abs(n int) int {
	if n < 0 {
		return -n
	}
	return n
}

有环链表相交

给定两个可能有环也可能无环的单链表， 头节点head 1和head 2。请实现一个函数，如果两个链表相交，请返回相交的第一个节点。如果不相交， 返回null

算法流程

1. 先判断两个链表是否都有环，都无环，则使用无环相交链表函数即可

2. 如果一个有环，一个无环，则不可能相交

3. 如果两个都有环，则有如下两种情况

   1. 成环的节点一样，则以成环的节点为终点，采用无环相交链表的算法可以得到交点

      

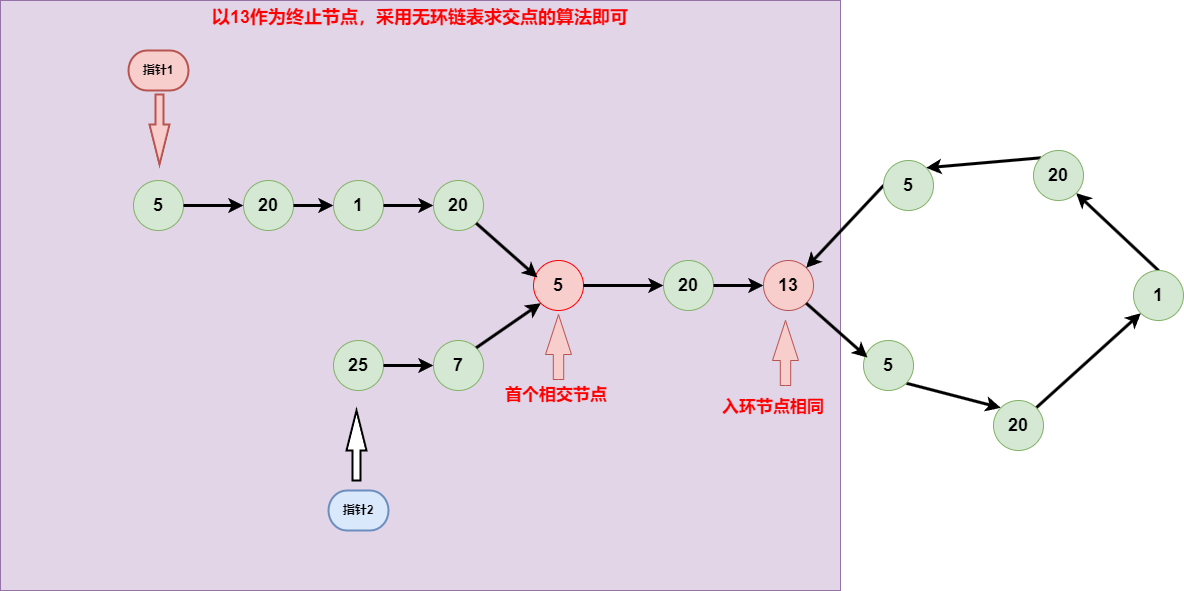
   2. 成环的节点不一样，有以下两种情况，判断以下两个节点是否在一个环内即可

      

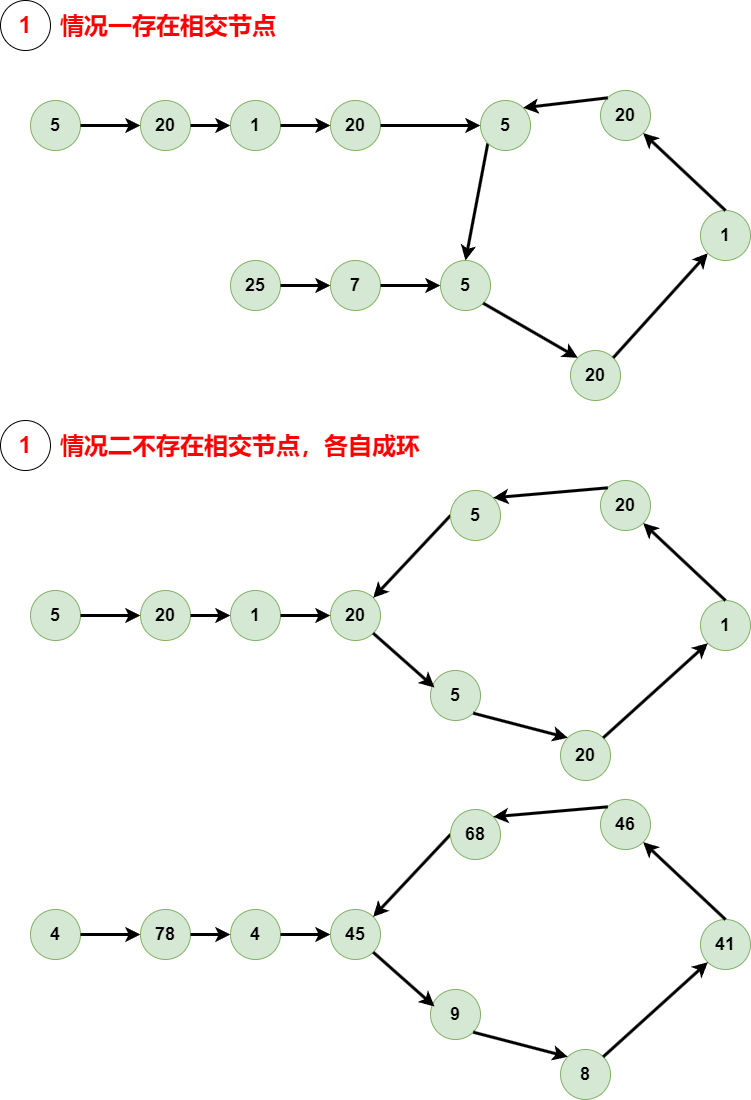
代码实现

func loopGetIntersectionNode(headA, headB *ListNode) *ListNode {
	if headA == nil || headB == nil {
		return nil
	}
	loop1, loop2 := detectCycle(headA), detectCycle(headB)
	if loop1 == nil && loop2 == nil {
		return getIntersectionNode(headA, headB)
	}
	if loop1 != nil && loop2 != nil {
		return bothLoop(headA, loop1, headB, loop2)
	}
	return nil
}

func bothLoop(headA, loopA, headB, loopB *ListNode) *ListNode {
	if loopA == loopB {
		p1, p2 := headA, headB
		n := 0
		for p1.Next != loopA {
			p1 = p1.Next
			n++
		}
		for p2.Next != loopA {
			p2 = p2.Next
			n--
		}
		if n < 0 {
			p1, p2 = p2, p1
		}
		n = abs(n)
		for n != 0 {
			p1 = p1.Next
			n--
		}
		for p1 != p2 {
			p1 = p1.Next
			p2 = p2.Next
		}
		return p1
	} else {
		cur := loopA.Next
		for cur != loopA {
			if cur == loopB {
				return loopA
			}
			cur = cur.Next
		}
		return nil
	}
}