🧩 二叉树最大宽度问题

在算法和数据结构中，有一类问题涉及到二叉树，而其中之一是求解二叉树的最大宽度。接下来我们将深入探讨这个问题以及它的应用场景、算法流程以及用Go语言实现的代码。

📚 题目及示例

考虑一个二叉树，我们定义树的宽度为从根节点到最远叶子节点的最长路径中的节点数。在这个问题中，我们需要求解给定二叉树的最大宽度。

示例：给定下面的二叉树：

      1
     / \
    3   2
   / \   \  
  5   3   9

该二叉树的宽度为 3，因为最后一层的节点数最多。

💡 应用场景

这个问题虽然看似简单，但在实际中有一些非常有用的应用场景，比如：

1. 网络路由器带宽分配：在路由器网络中，了解路由器能够同时处理的最大数据包数量是至关重要的。二叉树的最大宽度问题可以帮助优化路由器的带宽分配策略，以提高网络性能。

2. 并行计算：在并行计算中，我们需要有效地利用计算资源。求解二叉树的最大宽度可以帮助我们确定并行计算任务的最大并发量，从而更好地利用计算资源。

3. 数据库索引优化：数据库索引是数据库系统中重要的性能优化手段之一。通过求解二叉树的最大宽度，我们可以设计更加高效的数据库索引结构，提高数据库查询的效率。

🧠 算法流程

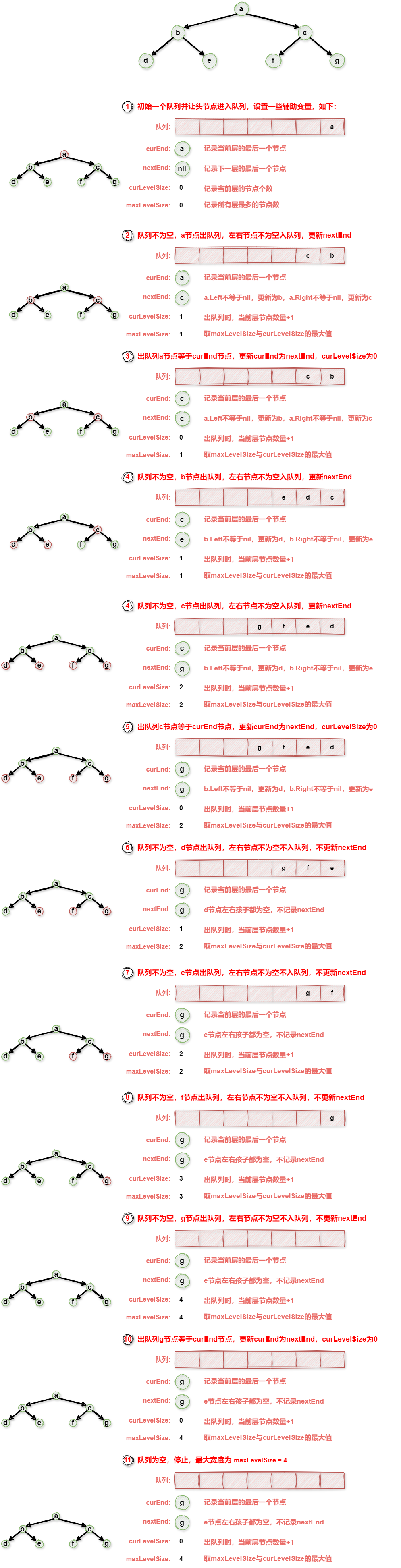
我们可以使用广度优先搜索（BFS）来解决这个问题。算法的具体步骤如下：

1. 初始化一个队列，并将根节点入队。
2. 使用一个计数器变量来记录当前层级的节点数目。
3. 在每一层的循环中，将当前层级的所有节点出队，并将它们的子节点入队。
4. 在每一层结束时，更新最大宽度的值为当前层级节点数目的最大值。
5. 重复步骤 3 和 4，直到队列为空。

算法图解：

💻 代码实现

代码

package binary_tree

import "container/list"

func TreeMaxWidth(head *TreeNode) int {
	res := 0
	if head == nil {
		return res
	}
	queue := list.New()
	var nextEnd *TreeNode
	curEnd := head
	queue.PushFront(head)
	curLevelSize := 0
	for queue.Len() > 0 {
		node := queue.Remove(queue.Back()).(*TreeNode)
		curLevelSize++
		if node.Left != nil {
			nextEnd = node.Left
			queue.PushFront(node.Left)
		}
		if node.Right != nil {
			nextEnd = node.Right
			queue.PushFront(node.Right)
		}
		if node == curEnd {
			res = max(curLevelSize, res)
			curLevelSize = 0
			curEnd = nextEnd
		}
	}
	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

测试

package binary_tree

import (
	"fmt"
	"testing"
)

func TestTreeMaxWidth(t *testing.T) {
	root := &TreeNode{Value:"a"}
	root.Left = &TreeNode{Value:"b"}
	root.Right = &TreeNode{Value:"c"}
	root.Left.Left= &TreeNode{Value:"d"}
	root.Left.Right= &TreeNode{Value:"e"}
	root.Right.Left= &TreeNode{Value:"f"}
	root.Right.Right= &TreeNode{Value:"g"}
	fmt.Println(TreeMaxWidth(root))
}