# 🌟校验完全二叉树🌳
完全二叉树是一种特殊的二叉树结构,它具有一些独特的性质。在完全二叉树中,除了最后一层外,每一层的节点都必须是满的,而且最后一层的节点都集中在树的左侧。
# 📈例子
为了更好地理解完全二叉树,让我们来看一个例子:
1
/ \
2 3
/ \ /
4 5 6
1
2
3
4
5
2
3
4
5
在这个例子中,这棵树是一个完全二叉树。每一层都是满的,除了最后一层的节点是从左到右填充的。
# 🧐应用
完全二叉树虽然在实际中并不是特别常见,但在某些场景下具有重要意义:
- 堆数据结构:堆是一种特殊的完全二叉树结构,常用于实现优先队列。在堆中,父节点的优先级总是大于或等于其子节点的优先级。
- 哈夫曼编码:哈夫曼树是一种特殊的二叉树,用于数据压缩中的哈夫曼编码。在哈夫曼树中,频率较低的字符位于树的底部,频率较高的字符位于树的顶部,这样可以实现最优的编码方案。
- 文件系统存储:在某些文件系统的实现中,树结构被用来组织文件和目录。完全二叉树可以用来表示某些存储优化的数据结构。
# 💼题目
给定一棵二叉树,设计一个算法来判断它是否是完全二叉树。
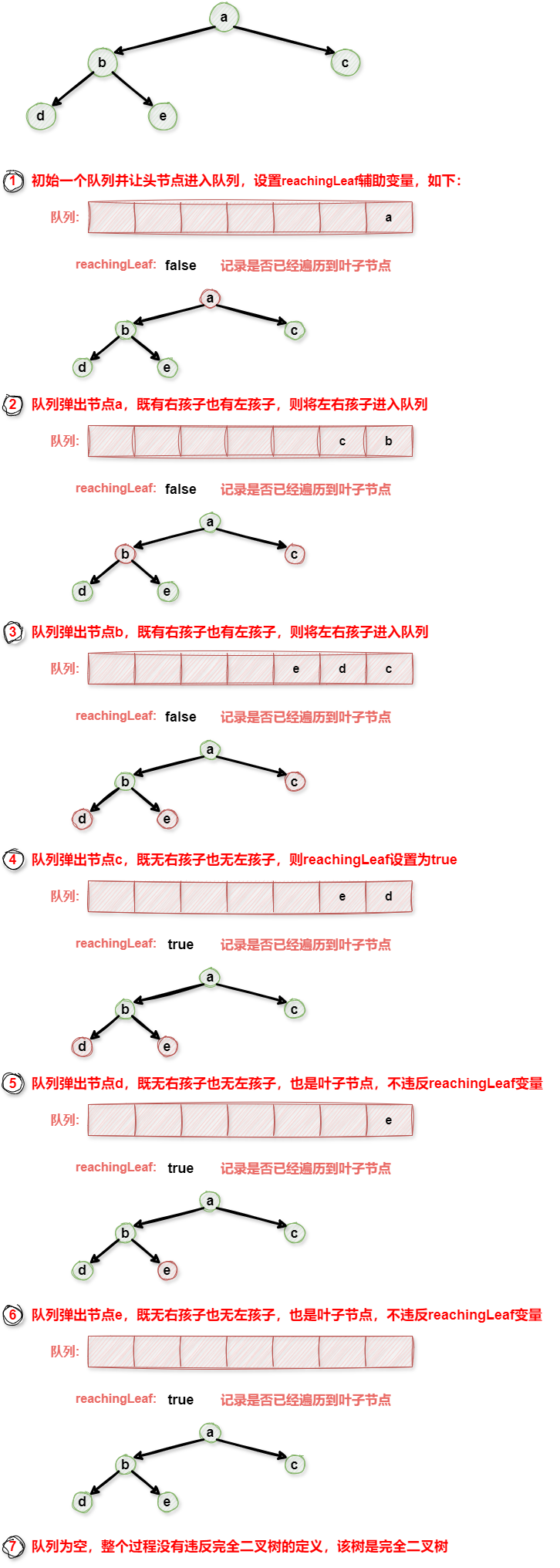
# 🚀算法流程
- 从树的根节点开始,进行层序遍历。
- 如果遇到一个节点的左子树为空,但右子树不为空,或者遇到一个节点的左右子树不全为空但右子树为空,则该树不是完全二叉树。
- 如果遇到一个节点的左子树为空,则接下来的所有节点都必须是叶子节点,否则该树不是完全二叉树。
- 如果遍历过程中未触发上述条件,则该树是完全二叉树。
# 🖥️Go语言实现
代码:
package binary_tree
import "container/list"
func IsCBT(root *TreeNode) bool {
if root == nil {
return true
}
queue := list.New()
queue.PushFront(root)
var meetLeaf bool
for queue.Len() > 0 {
n := queue.Remove(queue.Back()).(*TreeNode)
if n.Left == nil && n.Right != nil { // 有左孩子无右孩子,不满足完全二叉树的条件,直接返回
return false
}
if meetLeaf && (n.Left != nil || n.Right != nil) {
// 如果已经有过叶子节点了,后续必须都为叶子节点,否则返回false
return false
}
if n.Left != nil {
queue.PushFront(n.Left)
}
if n.Left != nil {
queue.PushFront(n.Right)
}
if n.Left == nil && n.Right == nil {
// 遇到叶子节点,将遇到叶子节点标记为true
meetLeaf = true
}
}
return true
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
调试:
package binary_tree
import (
"fmt"
"testing"
)
func TestIsCBT(t *testing.T) {
root := &TreeNode{Value:"a"}
root.Left = &TreeNode{Value:"b"}
root.Right = &TreeNode{Value:"c"}
root.Left.Left= &TreeNode{Value:"e"}
root.Left.Right= &TreeNode{Value:"f"}
//root.Right.Left= &TreeNode{Value:"g"}
root.Right.Right= &TreeNode{Value:"h"}
fmt.Println(IsCBT(root))
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17